핸즈온 머신러닝 제8장 차원 축소
머신러닝은 데이터들이 수천 수백만개의 특성(Features, columns)를 가지고 있는 경우가 많고, 많은 특성은 훈련을 느리게 하고, 과적합을 일으켜서 성능을 저하시킬 수 있습니다. 이러한 문제를 차원의 저주(curse of dimensionally)하고 합니다.
차원 축소는 실무에서, 효과가 없는 경우가 많고 오토인코더나 딥러닝의 신명망을 사용하면 이장의 다른 축소기법보다 효과적인 경우가 많습니다.
ADP나 빅분기 시험 등에서는 매우 자주 나오는 방법이므로 개념과 수식 이해가 필요합니다.
8.1 차원의 저주
차원의 저주(Curse of Dimensionality)는 차원이 증가할수록 데이터 분석과 머신러닝 모델의 성능이 악화되는 현상을 말합니다. 이는 주로 고차원 공간에서 데이터가 희소(sparse)해지고, 거리 기반 알고리즘의 효율이 급격히 떨어지기 때문에 발생합니다.
많은 머신러닝 알고리즘은 데이터 간 거리나 유사도에 기반합니다. 그러나 차원이 높아질수록 데이터 포인트들이 서로 멀어지고, 전체 공간 대비 밀도가 낮아지기 때문에 알고리즘이 유의미한 패턴을 잡기 어려워집니다.
이러한 희소성은 다음과 같은 문제를 유발합니다:
- 과적합: 일부 데이터 샘플에 모델이 지나치게 의존
- 계산 비용 증가: 훈련 시간 및 메모리 사용량 증가
- 일반화 성능 저하: 테스트 데이터에 대한 예측 정확도 감소
책의 설명
- 1차원: 길이 1인 선을 10등분 → 각 구간의 길이는 0.1
- 2차원: 0.1 × 0.1 = 0.01 크기의 격자를 만들려면 총 100개 필요
- 100차원: $0.1^{100}$ → 거의 0에 가까움 (즉, 같은 밀도를 유지하려면 $10^{100}$ 개의 데이터 필요)
→ 차원이 증가하면 공간이 기하급수적으로 확장되며, 같은 밀도를 유지하려면 엄청난 수의 데이터가 필요하게 됩니다.
8.2 차원 축소를 위한 접근
8.2.1 투영
투영(Projection)은 차원 축소의 기본적인 방식 중 하나로, 고차원 데이터를 저차원 평면에 직선적으로 내리는 방식입니다. 이 개념은 특히 PCA(주성분 분석)의 핵심 원리이기도 합니다.
예를 들어, 네비게이션에서 3차원 지형을 2차원 지도에 투영하여 경로를 확인하는 것처럼, 복잡한 고차원 데이터를 더 단순한 공간에 표현할 수 있습니다.
이 방법은 데이터의 분산이 가장 큰 방향(축)을 선택하여, 정보 손실을 최소화하면서 데이터 구조를 최대한 보존하려는 목적을 가집니다. 투영을 통해 차원을 줄이면서도 주요 특성을 유지할 수 있는 효과적인 방식입니다.
다음 코드는 책에서 3차원 데이터셋을 PCA로 2차원으로 투영해서 줄인 결과를 시각화하는 코드를 일부 수정하였습니다.
원본 코드 : https://github.com/rickiepark/handson-ml3
import matplotlib.pyplot as plt
from scipy.spatial.transform import Rotation
from sklearn.decomposition import PCA
import koreanize_matplotlib
# 1. 데이터 생성 (3D 타원 + 회전 + 노이즈 추가)
np.random.seed(42)
m = 60
angles = (np.random.rand(m) ** 3 + 0.5) * 2 * np.pi
X = np.zeros((m, 3))
X[:, 0], X[:, 1] = np.cos(angles), np.sin(angles) * 0.5
X += 0.28 * np.random.randn(m, 3) # 노이즈
X = Rotation.from_rotvec([np.pi/29, -np.pi/20, np.pi/4]).apply(X)
X += [0.2, 0, 0.2] # 약간 이동
# 2. PCA로 2D 투영 및 역투영
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)
X3D_inv = pca.inverse_transform(X2D)
# 3. 투영 평면 계산
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
axes = [-1.4, 1.4, -1.4, 1.4, -1.1, 1.1]
x1, x2 = np.meshgrid(np.linspace(axes[0], axes[1], 10), np.linspace(axes[2], axes[3], 10))
w1, w2 = np.linalg.solve(Vt[:2, :2], Vt[:2, 2])
z = w1 * (x1 - pca.mean_[0]) + w2 * (x2 - pca.mean_[1]) - pca.mean_[2]
# 4. 평면 위/아래 샘플 분리
X3D_above = X[X[:, 2] >= X3D_inv[:, 2]]
X3D_below = X[X[:, 2] < X3D_inv[:, 2]]
# 5. 시각화: 가로 2개 subplot (3D, 2D)
fig = plt.figure(figsize=(14, 6))
# ─── 5.1 3D 투영 시각화 ───
ax3d = fig.add_subplot(1, 2, 1, projection="3d")
ax3d.plot_surface(x1, x2, z, alpha=0.1, color="b") # 투영 평면
ax3d.plot(X3D_inv[:, 0], X3D_inv[:, 1], X3D_inv[:, 2], "b+") # 투영점
# 투영선 + 샘플 점
for i in range(m):
ax3d.plot([X[i][0], X3D_inv[i][0]], [X[i][1], X3D_inv[i][1]], [X[i][2], X3D_inv[i][2]], "r--" if X[i, 2] >= X3D_inv[i, 2] else ":")
ax3d.plot(X3D_above[:, 0], X3D_above[:, 1], X3D_above[:, 2], "ro")
ax3d.plot(X3D_below[:, 0], X3D_below[:, 1], X3D_below[:, 2], "ro", alpha=0.3)
# 축 설정
ax3d.set_xlabel("$x_1$")
ax3d.set_ylabel("$x_2$")
ax3d.set_zlabel("$x_3$")
ax3d.set_xlim(axes[0:2])
ax3d.set_ylim(axes[2:4])
ax3d.set_zlim(axes[4:6])
ax3d.set_title("3D에서 평면으로의 투영")
# ─── 5.2 2D 투영된 평면 시각화 ───
ax2d = fig.add_subplot(1, 2, 2, aspect='equal')
ax2d.plot(X2D[:, 0], X2D[:, 1], "b.")
ax2d.plot([0], [0], "bo") # 원점
ax2d.arrow(0, 0, 1, 0, head_width=0.05, length_includes_head=True,
head_length=0.1, fc='b', ec='b', linewidth=3)
ax2d.arrow(0, 0, 0, 1, head_width=0.05, length_includes_head=True,
head_length=0.1, fc='b', ec='b', linewidth=1)
ax2d.set_xlabel("$z_1$")
ax2d.set_ylabel("$z_2$", rotation=0)
ax2d.set_yticks([-0.5, 0, 0.5, 1])
ax2d.grid(True)
ax2d.set_title("2D PCA 투영 결과")
plt.tight_layout()
plt.show()
8.2.2 매니폴드 학습
매니폴드 학습(Manifold Learning)은 비선형 차원 축소 방법 중 하나로, 선형 투영 방식(PCA 등)의 한계를 극복하기 위한 접근입니다.
매니폴드(manifold)란 고차원 공간 속에 내재된 저차원 곡면 구조를 의미합니다.
예를 들어, 2차원 종이가 구겨져 3차원 공간에 존재한다면, 그 종이는 여전히 본질적으로 2차원 구조를 갖고 있는 매니폴드입니다. 이 종이를 구부러진 구조를 따라 잘 펼치면, 다시 간단한 2차원 평면 구조로 표현할 수 있습니다.
이러한 사고는 매니폴드 가정(Manifold Assumption)에 기반합니다.
“고차원 데이터는 본질적으로 저차원 곡면(매니폴드) 위에 존재한다.”
즉, 단순히 데이터를 직선적으로 자르듯 투영하는 것이 아니라, 내재된 곡면 구조를 따라 저차원 공간으로 펼치는 것이 더 적절하다는 생각에서 출발합니다.
또한, "manifold"는 영어로 다양한, 다차원적인이라는 의미를 가지며, 라틴어 manu foldere(손으로 접다)에서 유래했습니다. 이 의미가 확장되어, 머신러닝에서는 저차원 곡면이 고차원 데이터 공간 안에 접힌 상태로 존재한다는 개념으로 사용됩니다.
매니폴드 학습은 이 접힌 구조를 다시 펴서 본래의 저차원 공간으로 복원하는 기법입니다.
아래 코드는 3D 스위스롤 즉 곡면위에 데이터가 나선형으로 노란색과 초록색 클래스가 말려있는 구조입니다.
PCA로 투영한 결과와 매니폴드(LLE)로 데이터를 펼친 결과를 비교하였습니다.
2차원 공간에서 PCA는 두 클래스가 여전히 겹치고 분리가 어렵지만, 매니폴드는 두 클래스가 좀더 명확하게 구분됩니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.decomposition import PCA
from sklearn.manifold import LocallyLinearEmbedding
# 1. 스위스롤 데이터 생성
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
# 2. 분류 조건 정의 (예: 곡면 위에서 직선 분리)
# 조건: 2(t - 4) > x₂
condition = 2 * (t - 4) > X[:, 1]
labels = condition.astype(int)
# 3. 차원 축소
X_pca = PCA(n_components=2).fit_transform(X)
X_lle = LocallyLinearEmbedding(n_components=2, n_neighbors=12, random_state=42).fit_transform(X)
# 4. 시각화 (1x3)
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 4-1. 원본 3D
ax = axes[0]
ax = fig.add_subplot(1, 3, 1, projection='3d')
ax.scatter(X[labels == 0, 0], X[labels == 0, 1], X[labels == 0, 2], c="y", marker="^", label="Class 0")
ax.scatter(X[labels == 1, 0], X[labels == 1, 1], X[labels == 1, 2], c="g", marker="s", label="Class 1")
ax.set_title("원본 3D 스위스롤")
ax.view_init(10, -70)
# 4-2. PCA 결과
axes[1].scatter(X_pca[labels == 0, 0], X_pca[labels == 0, 1], c="y", marker="^", label="Class 0")
axes[1].scatter(X_pca[labels == 1, 0], X_pca[labels == 1, 1], c="g", marker="s", label="Class 1")
axes[1].set_title("PCA 투영 결과")
axes[1].set_xlabel("PC1")
axes[1].set_ylabel("PC2")
axes[1].grid(True)
# 4-3. 매니폴드 (LLE)
axes[2].scatter(X_lle[labels == 0, 0], X_lle[labels == 0, 1], c="y", marker="^", label="Class 0")
axes[2].scatter(X_lle[labels == 1, 0], X_lle[labels == 1, 1], c="g", marker="s", label="Class 1")
axes[2].set_title("LLE (매니폴드 학습)")
axes[2].set_xlabel("z1")
axes[2].set_ylabel("z2")
axes[2].grid(True)
plt.tight_layout()
plt.show()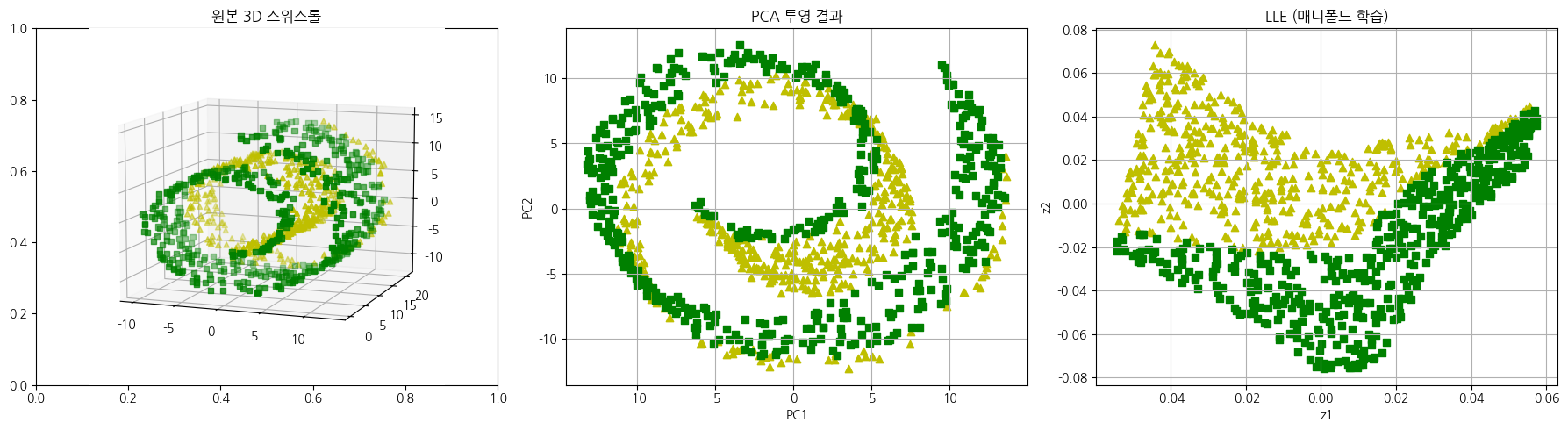
8.3 주성분 분석
주성분 분석(PCA, Principal component analysis)은 가장 인기 있는 차원 축소 방법 중 하나로, 데이터에 가장 가까운 초명편을 정의한 다음 데이터를 투영시키는 방법입니다.
8.3.1 분산 보전
PCA는 데이터의 “분산(variance)”을 가장 잘 보존하는 축을 찾는 방법입니다.
즉, 정보를 가장 많이 담고 있는 방향으로 데이터를 투영하여 차원을 줄이되, 정보 손실을 최소화하는 것이 목적입니다.
- 분산은 데이터의 퍼짐 정도이고 데이터가 한 방향으로 많이 퍼져 있다는 것은 그 방향에 중요한 정보가 많다는 뜻입니다.
- 데이터를 투영하는 축은 분산이 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실되므로 합리적으로 보입니다.
책 내용으로 github의 코드를 다시 작성한 것으로, 분산을 최대화 하는 c1을 투영축으로 선택하는 것이 가장 좋다는 시각화 코드입니다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(3)
angle = np.pi / 5
stretch = 5
m = 200
# 1. 원형 분포 → 스트레치 → 회전
X = np.random.randn(m, 2) / 10
X = X @ np.diag([stretch, 1])
rotation = np.array([[np.cos(angle), np.sin(angle)],
[-np.sin(angle), np.cos(angle)]])
X = X @ rotation
# 2. 투영 방향 정의 (주성분 후보 벡터)
c1 = np.array([np.cos(angle), np.sin(angle)])
c2 = np.array([np.cos(angle - 2 * np.pi / 6), np.sin(angle - 2 * np.pi / 6)])
c3 = np.array([np.cos(angle - np.pi / 2), np.sin(angle - np.pi / 2)])
# 3. 각 축으로 투영
projections = [X @ v.reshape(-1, 1) for v in [c1, c2, c3]]
# 4. 시각화
fig = plt.figure(figsize=(8, 4))
# 4-1. 원본 데이터 및 벡터 시각화
ax = plt.subplot2grid((3, 2), (0, 0), rowspan=3)
ax.plot(X[:, 0], X[:, 1], "ro", alpha=0.5)
for vec, style, label in zip([c1, c2, c3], ["-", "--", ":"], ["$c_1$", None, "$c_2$"]):
ax.plot([-1.4, 1.4], [-1.4 * vec[1] / vec[0], 1.4 * vec[1] / vec[0]], f"k{style}", linewidth=2)
ax.arrow(0, 0, vec[0], vec[1], head_width=0.1, length_includes_head=True,
head_length=0.1, fc='b', ec='b', linewidth=2 if style == "-" else 1, alpha=0.9)
if label:
ax.text(vec[0] + 0.1, vec[1] - 0.05, label, color="blue")
ax.set_xlim(-1.4, 1.4)
ax.set_ylim(-1.4, 1.4)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$", rotation=0)
ax.grid()
# 4-2. 투영 결과 시각화
for i, proj in enumerate(projections):
ax = plt.subplot2grid((3, 2), (i, 1))
ax.plot(proj[:, 0], np.zeros(m), "ro", alpha=0.3)
ax.plot([-2, 2], [0, 0], f"k{['-', '--', ':'][i]}", linewidth=2)
ax.set_xlim(-2, 2)
ax.set_ylim(-1, 1)
ax.set_yticks([])
if i < 2:
ax.set_xticklabels([])
if i == 2:
ax.set_xlabel("$z_1$")
ax.grid()
plt.tight_layout()
plt.show()

8.3.2 주성분
PCA는 데이터에서 분산이 최대인 첫번째 축을 찾습니다.
이후, 첫번째 축을 직교하는 남은 분산을 최대화 하는 두번째 축을 찾고, 이전의 두축을 직교하는 세번째 축을 찾는 식으로 입력 Feature와 같은 차원의 축을 찾습니다.
이 새로운 축을 주성분이라고 합니다. 주성분은 고유값 분해 또는 특이값 분해로 찾을 수 있습니다.
아래는 고유값 분해의 수식입니다.
$X = U Σ V^T$
여기서 $V^T$가 모든 주성분의 고유벡터 V가 포함된 주성분 행렬입니다.
아래 코드는 iris에서 2개의 주성분을 출력하는 코드입니다.
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
Vt[0], Vt[1](array([ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ]),
array([-0.65658877, -0.73016143, 0.17337266, 0.07548102]))
8.3.3 d차원으로 투영
주성분은 분산을 최대화 하는 방향입니다.
원본 데이터를 원하는 d차원으로 투영하여, 새로운 d차원의 feature로 축소 시킬 수 있습니다.
새로운 Feature는 $X_pca = X@V.T$로 투영할 수 있습니다.
많이 사용되는 iris는 4개 차원의 150개의 데이터인데, 2개 차원으로 축소 후 5개의 샘플만 출력하는 코드입니다.
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
X_pca = X_centered@Vt[:2].T
X_pca[:5]array([[-2.68412563, -0.31939725],
[-2.71414169, 0.17700123],
[-2.88899057, 0.14494943],
[-2.74534286, 0.31829898],
[-2.72871654, -0.32675451]])
8.3.4 사이킷 런 사용하기
sklearn에서 PCA를 제공합니다.
n_components 하이퍼 파라미터로 주성분의 개수를 지정할 수 있습니다.
사이킷런의 PCA는 자동으로 데이터를 중앙으로 맞춰줍니다.
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
X, y = load_iris(return_X_y=True)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
X_pca[:5]array([[-2.68412563, 0.31939725],
[-2.71414169, -0.17700123],
[-2.88899057, -0.14494943],
[-2.74534286, -0.31829898],
[-2.72871654, 0.32675451]])고유 벡터가 방향만 사용하기 때문에 부호가 일치하지 않는 것을 제외하면 2개의 결과가 동일함을 알 수 있습니다.
아래는 sklearn의 PCA와 고유값 분해 및 SVD로 주성분 분석을 수행 후 결과가 동일한지 확인하는 코드입니다.
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import numpy as np
# 1. 데이터 불러오기 및 표준화
X, y = load_iris(return_X_y=True)
X_scaled = StandardScaler().fit_transform(X)
# 2. 고유값 분해 방식 (공분산 행렬)
cov = np.cov(X_scaled.T)
eigval, V_eig = np.linalg.eig(cov)
X_pca_eig = X_scaled @ V_eig # shape (150, 4)
# 3. SVD 방식
U, s, Vt = np.linalg.svd(X_scaled, full_matrices=False)
X_pca_svd = X_scaled @ Vt.T # shape (150, 4)
# 4. sklearn PCA
pca = PCA(n_components=4)
X_pca_sklearn = pca.fit_transform(X_scaled) # shape (150, 4)
# 5. 세 결과 비교 (부호 반전 허용)
def equal_up_to_sign(A, B):
"""두 행렬이 부호만 다를 경우 동일하다고 간주"""
return np.allclose(np.abs(A), np.abs(B), atol=1e-5)
# 6. 결과 출력
print("고유값 분해 vs SVD:", equal_up_to_sign(X_pca_eig, X_pca_svd))
print("고유값 분해 vs sklearn PCA:", equal_up_to_sign(X_pca_eig, X_pca_sklearn))
print("SVD vs sklearn PCA:", equal_up_to_sign(X_pca_svd, X_pca_sklearn))고유값 분해 vs SVD: True 고유값 분해 vs sklearn PCA: True SVD vs sklearn PCA: True
8.3.5 설명된 분산의 비율
sklearn의 PCA에 explained_variane_ratio_ 변수에 주성분의 설명된 분산의 비율을 나타냅니다.
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
X, y = load_iris(return_X_y=True)
pca = PCA(n_components=2)
pca.fit(X)
pca.explained_variance_ratio_array([0.92461872, 0.05306648])
첫번째 주성분이 전체의 92%를 설명하고, 두번째 주성분이 5%의 주성분을 설명하고 있음을 알려줍니다.
8.3.6 적절한 차원 수 선택
PCA 적용 시 몇 개의 주성분을 사용할지 결정하는 방법을 다룹니다.
전체 주성분 중 몇 개(d)만 선택하면 충분할까?
PCA는 차원 축소를 목적으로 하지만, 너무 많이 줄이면 정보 손실, 너무 적게 줄이면 축소의 의미가 없기 때문에 균형이 필요합니다.
보통 아래 2가지 방법을 사용합니다.
| 1️⃣ 누적 설명 분산 기준 | 전체 분산 중 일정 비율(예: 95%) 이상을 설명하는 주성분 수 선택 |
| 2️⃣ Scree Plot (스크리 플롯) | 분산 감소 기울기가 급격히 완만해지는 지점(elbow point)에서 주성분 수 결정 |
아래 코드는 누적비율이 95% 이상이 되는 주성분을 선택하는 방법과, scree plot을 그리는 방법에 대한 코드입니다.
95%는 explained_variance_ratio_의 cumsum으로 확인 가능하지만, n_components 에서 0과 1사이의 비율로 결정하는 것이 더 편리합니다. scree plot은 급격히 완만 해지는 포인트를 선택하는 방법이지만, 실제 데이터로 잘 보이지 않는 경우가 많습니다.
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np
# 1. MNIST (digits) 데이터셋 불러오기
X, y = load_digits(return_X_y=True)
# 2. 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 3. PCA 전체 학습
pca_full = PCA()
X_pca_full = pca_full.fit_transform(X_scaled)
# 3-1. 누적 설명 분산 계산하여 95% 이상 보존하는 주성분 수 계산
cumsum = np.cumsum(pca_full.explained_variance_ratio_)
n_95 = np.argmax(cumsum >= 0.95) + 1 # 최소 개수
# 3-2. n_components = 0.95로 설정 시 자동 선택되는 주성분 수
pca_95 = PCA(n_components=0.95)
X_pca_95 = pca_95.fit_transform(X_scaled)
n_components_95 = pca_95.n_components_
# 3-3. Scree Plot
plt.figure(figsize=(8, 5))
plt.plot(np.arange(1, len(pca_full.explained_variance_ratio_) + 1),
np.cumsum(pca_full.explained_variance_ratio_), marker='o')
plt.axvline(n_95, color='r', linestyle='--', label=f"95% cut-off: {n_95} components")
plt.title("Scree Plot - MNIST (Digits Dataset)")
plt.xlabel("Number of Components")
plt.ylabel("Explained Variance Ratio")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 결과 요약
n_95, n_components_95
(40, 40)
8.3.7 압축을 위한 PCA
PCA는 단순 차원 축소용 기법이 아닌 손실 압축 기법으로도 사용할 수 있습니다.
고차원 정보에서 저장공간 절약 노이즈 제거에 유용합니다.
pca로 transform후 inverse_trainform으로 원래의 차원으로 복원 할 수 있습니다.
원본 데이터와 복원된 데이터의 오차를 재구성 오차하고 합니다.
압축 : $ Z=Xcentered⋅Vd$
복원 : $\hat X=Z⋅V_d^⊤+mean$
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
# 데이터 로딩
digits = load_digits()
X, y = digits.data, digits.target
# 정규화
# X_scaled = StandardScaler().fit_transform(X)
# PCA 압축 (95% 분산 유지)
pca = PCA(n_components=0.95)
X_pca = pca.fit_transform(X)
X_reconstructed = pca.inverse_transform(X_pca)
# 차원 수 정보
original_shape = X.shape
compressed_shape = X_pca.shape
reconstructed_shape = X_reconstructed.shape
# 원본 이미지와 복원 이미지 비교 (10개만)
n = 10
fig, axes = plt.subplots(2, n, figsize=(12, 3))
for i in range(n):
# 원본
axes[0, i].imshow(X[i].reshape(8, 8), cmap="binary")
axes[0, i].axis("off")
# 복원
axes[1, i].imshow(X_reconstructed[i].reshape(8, 8), cmap="binary")
axes[1, i].axis("off")
axes[0, 0].set_ylabel("Original", fontsize=12)
axes[1, 0].set_ylabel("Reconstructed", fontsize=12)
plt.suptitle("PCA Compression and Reconstruction (95% Variance)", fontsize=14)
plt.tight_layout()
plt.show()
# 결과 반환
original_shape, compressed_shape, reconstructed_shape(1797, 64), (1797, 29), (1797, 64))
글자가 흐릿하긴 하지만, 64개에서 29개로 차원이 축소되어 압축되었습니다.
8.3.8 랜덤 PCA
랜덤 PCA (Randomized PCA)는 큰 데이터셋에서 PCA를 더 빠르게 수행하기 위한 근사 기법입니다.
일반적인 PCA는 SVD(특이값 분해) 또는 고유값 분해를 사용하는데 특성의 수가 많으면 매우 느려집니다.
고차원 행렬 에 무작위 투영(Random Projection)을 적용하여, 저차원 근사 행렬에 대해 SVD 수행하여, 적은 계산으로 가장 중요한 주성분만 근사합니다.
sklearn.PCA(svd_solver="randomized")로 랜덤 PCA를 사용할 수 있습니다.
from sklearn.decomposition import PCA
# 일반 PCA (기본은 'auto')
pca1 = PCA(n_components=100, svd_solver="full")
# 랜덤 PCA
pca2 = PCA(n_components=100, svd_solver="randomized", random_state=42)
8.3.9 점진적 PCA
점진적 PCA (Incremental PCA, IPCA)는 대용량 데이터셋을 메모리에 한 번에 올릴 수 없을 때 사용하는 PCA 방식입니다.
일반 PCA의 경우 모든 데이터를 메모리에 로드 한 후 한번에 전체 행렬로 PCA를 수행 대규모 데이터에는 부적합니다.
IPCA는 미니배치(batch)단위로 순차적으로 업데이트하며 PCA를 수행합니다.
한 번에 전체 데이터를 보지 않고, 작은 배치로 나눠서 학습하고, partial_fit() 메서드를 반복적으로 호출하여 누적 학습합니다.
내부적으로 배치마다 평균과 공분산을 업데이트합니다.
데이터를 배치를 사용할 때 numpy의 memmap과 같이 사용할 수 있습니다.
numpy.memmap은 매우 큰 배열을 다룰 때 사용하는 메모리 매핑(mmap) 기법입니다.
즉 , 전체 배열을 RAM에 올리지 않고, 디스크 파일을 메모리처럼 접근할 수 있게 합니다.
IPCA는 데이터를 배치(batch) 단위로 순차적으로 학습하므로, 전체 데이터를 디스크에서 한 번에 불러올 필요 없이, memmap으로 조각 조각 불러오면서 학습할 수 있습니다.
IncrementalPCA(
n_components=None, # 주성분 개수 (default=모든 성분)
batch_size=None # 한 번에 처리할 데이터 샘플 수
)
from sklearn.decomposition import IncrementalPCA
ipca = IncrementalPCA(n_components=100, batch_size=2000)
for i in range(0, len(X), 2000):
ipca.partial_fit(X[i:i+2000])
X_pca = ipca.transform(X)
다음은 mmap과 IPCA를 같이 사용한 예제입니다. MNINT를 mmap으로 저장 후 다시 load하였습니다.
from sklearn.datasets import fetch_openml
from sklearn.decomposition import IncrementalPCA
from sklearn.preprocessing import StandardScaler
import numpy as np
import os
import matplotlib.pyplot as plt
# 1. MNIST 데이터 로딩
X, y = fetch_openml('mnist_784', as_frame=False, parser="auto", return_X_y=True)
# 2. memmap으로 저장
filename = 'mnist.mmap'
if not os.path.exists(filename):
fp = np.memmap(filename, dtype='float32', mode='write', shape=X.shape)
fp[:] = X
fp.flush()
# 3. memmap으로 다시 읽기
X_memmap = np.memmap(filename, dtype='float32', mode='r', shape=X.shape)
batch_size = 2000
# 4. IncrementalPCA 수행
ipca = IncrementalPCA(n_components=100, batch_size=batch_size)
for i in range(0, X_memmap.shape[0], batch_size):
ipca.partial_fit(X_memmap[i:i+batch_size])
# 5. 일부 샘플 변환
X_pca = ipca.transform(X_memmap[:10000])
X_reconstructed = ipca.inverse_transform(X_pca)
# 원본 이미지와 복원 이미지 비교 (10개만)
n = 10
fig, axes = plt.subplots(2, n, figsize=(12, 3))
for i in range(n):
# 원본
axes[0, i].imshow(X[i].reshape(28, 28), cmap="binary")
axes[0, i].axis("off")
# 복원
axes[1, i].imshow(X_reconstructed[i].reshape(28, 28), cmap="binary")
axes[1, i].axis("off")
axes[0, 0].set_ylabel("Original", fontsize=12)
axes[1, 0].set_ylabel("Reconstructed", fontsize=12)
plt.suptitle("PCA Compression and Reconstruction (n_components=100)", fontsize=14)
plt.tight_layout()
plt.show()
8.4 랜덤 투영
랜덤 투영(Random Projection)은 차원을 축소하면서도 데이터 간 거리를 대략적으로 유지할 수 있는 기법입니다.
Johnson–Lindenstrauss Lemma 이론에 기반하는데 고차원 데이터를 무작위로 낮은 차원에 투영해도, 점들 간의 거리는 거의 유지된다.
고차원 공간에서는 많은 방향이 비슷하게 퍼져있고 , 무작위 랜덤 투영을 여러 번 수행해보면 대부분은 데이터 구조를 크게 왜곡하지 않고 랜덤한 투영이 어느정 괜찮은 방향일 확률이 상당히 높다는 내용입니다.
Johnson–Lindenstrauss Lemma는 n_samples개의 점을 ε(eps) 이내의 거리 왜곡으로 보존하기 위해 필요한 최소 차원 d는 다음을 만족해야 합니다:
$d≥\frac{ 4ln(n) }{\frac{ε^2}{2}−{ε^3}{3}}$
위 수식을 계산 하는 것이 johnson_lindenstrauss_min_dim입니다. 5000개의 샘플을 거리 왜곡 10% 이하로 보존하려면 7,300개의 차원으로 투영이 필요하다는 의미입니다.
from sklearn.random_projection import johnson_lindenstrauss_min_dim
d = johnson_lindenstrauss_min_dim(n_samples=5000, eps=0.1)
d7300
다음 코드는 랜덤 투영을 수동으로 차원축소 한것과 sklearn의 GaussianRandomProjection을 사용하여 차원 축소의 비교입니다.
10000개중 7894개로 차원을 축소하였고, 거리 왜곡을 계산 시 허용율 0.1보다 작은 0.06의 왜곡이 계산되었습니다.
import numpy as np
from sklearn.datasets import make_classification
from sklearn.random_projection import johnson_lindenstrauss_min_dim, GaussianRandomProjection
from sklearn.metrics import pairwise_distances
import pandas as pd
# 거리 변화량 계산 (상대 오차)
def compute_relative_error(original, reduced):
return np.mean(np.abs(original - reduced) / (original + 1e-10))
n=20000
m=10000
X_high, _ = make_classification(n_samples=n, n_features=m, random_state=42)
X_high = X_high.astype(np.float16)
# 거리 왜곡 허용률
eps = 0.1
# 최소 차원 수 계산
min_dim_high = johnson_lindenstrauss_min_dim(n_samples=10000, eps=eps)
print(f"샘플 수: {n:,}, 특성 수: {m:,}, 축소된 특성 수: {min_dim_high}, 거리 왜곡 허용률: {eps}")
# 수동 투영
np.random.seed(42)
P_high = np.random.randn(min_dim_high, X_high.shape[1]).astype(np.float32) / np.sqrt(min_dim_high)
X_proj_manual_high = X_high @ P_high.T
# GaussianRandomProjection 적용
grp_high = GaussianRandomProjection(n_components=min_dim_high, random_state=42)
X_proj_sklearn_high = grp_high.fit_transform(X_high)
# 거리 비교 (상위 200개 샘플만)
original_dist_high = pairwise_distances(X_high[:200])
manual_dist_high = pairwise_distances(X_proj_manual_high[:200])
sklearn_dist_high = pairwise_distances(X_proj_sklearn_high[:200])
# 거리 왜곡 계산
error_manual_high = compute_relative_error(original_dist_high, manual_dist_high)
error_sklearn_high = compute_relative_error(original_dist_high, sklearn_dist_high)
# 결과 요약
print('결과 요약')
print("Manual Random vs GaussianRandom Projection outputs are close:",
np.allclose(np.abs(X_proj_manual_high), np.abs(X_proj_sklearn_high), atol=1e-3))
print('거리 왜곡 계산')
print('Manual Random Projection : ',error_manual_high)
print('GaussianRandomProjection :',error_sklearn_high)샘플 수: 20,000, 특성 수: 10,000, 축소된 특성 수: 7894, 거리 왜곡 허용률: 0.1
결과 요약
Manual Random vs GaussianRandom Projection outputs are close: True
거리 왜곡 계산
Manual Random Projection : 0.006167613655229116
GaussianRandomProjection : 0.006167616283281289
SparseRandomProjection은 고차원 데이터를 저차원으로 축소하는 랜덤 투영 기법 중 하나로,
GaussianRandomProjection과 유사하지만 희소(sparse)한 투영 행렬을 사용해 메모리와 연산을 절약하는 것이 특징입니다.
SparseRandomProjection은 대규모 고차원 데이터에서 매우 유용합니다.
CA나 Gaussian 방식보다 메모리를 훨씬 적게 사용하고 빠르고 가볍지만, 약간의 거리 왜곡 가능성은 있습니다
from sklearn.random_projection import SparseRandomProjection
srp = SparseRandomProjection(n_components=5000, random_state=42)
X_srp = srp.fit_transform(X_high)
8.5 지역 선형 임베딩
지역 선형 임베딩(Local Linear Embedding, LLE)은 비선형 차원 축소 기법 중 하나입니다.
특히 매니폴드 학습(manifold learning)에서 대표적인 방법으로, 데이터가 고차원 공간에 있으나 저차원 곡면(매니폴드) 위에 있다고 가정할 때 매우 효과적입니다.
sklearn.manifold.LocallyLinearEmbedding은 Scikit-learn에서 제공하는 지역 선형 임베딩(Local Linear Embedding, LLE) 알고리즘 구현입니다.
from sklearn.manifold import LocallyLinearEmbedding| 파라미터 | 설명 |
| n_neighbors | 각 점 주변의 이웃 수 (기본: 5). 너무 작으면 잡음 민감, 너무 크면 비선형 구조를 무시 |
| n_components | 축소할 차원 수 |
| method | 'standard', 'modified', 'hessian', 'ltsa' Defalut: 'standard' (원래 LLE) |
| eigen_solver | 'auto', 'dense', 'arpack' |
| random_state | 랜덤 시드 |
| modified_tol, hessian_tol, reg | 각 기법의 정규화 또는 수치 안정화 옵션 |
| 속성 | 설명 |
| embedding_ | 임베딩된 결과 (n_samples × n_components 배열) |
| reconstruction_error_ | 재구성 오차 (원본 vs. 근사된 점들의 차이) |
스위스롤 데이터셋으로, LLM으로 차원 축소한 결과입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
# 1. 스위스롤 데이터 생성
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
# 2. LLE 적용
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_lle = lle.fit_transform(X)
# 3. 시각화 (3D 원본 + 2D 변환 결과)
fig = plt.figure(figsize=(12, 5))
# (1) 원본 3D 스위스롤
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.Spectral, s=10)
ax1.set_title("Original 3D Swiss Roll")
# (2) 2D LLE 결과
ax2 = fig.add_subplot(1, 2, 2)
scatter = ax2.scatter(X_lle[:, 0], X_lle[:, 1], c=t, cmap=plt.cm.Spectral, s=10)
ax2.set_title("2D Unfolded via LLE")
ax2.set_xlabel("z1")
ax2.set_ylabel("z2")
plt.colorbar(scatter, ax=[ax1, ax2], shrink=0.5, label="Color by $t$")
plt.show()
LLE 단계
1. 이웃 찾기
- 각 샘플에 대해 k-최근접 이웃(k-NN)을 찾습니다.
2. 선형 가중치 계산
- 각 샘플 $x_i$를 이웃 샘플들의 선형 결합으로 근사합니다.
- 즉, 가중치 $w_{ij}$를 구해 아래 수식을 최소화합니다:
$\min_{w_{ij}} \sum_i \left\| \mathbf{x}_i - \sum_{j \in \mathcal{N}(i)} w_{ij} \mathbf{x}_j \right\|^2$
조건: $\sum_{j \in \mathcal{N}(i)} w_{ij} = 1$
3. 저차원 좌표 구성
- 위에서 구한 $w_{ij}$를 그대로 유지하면서, 저차원에서 새로운 포인트 $z_i$를 찾습니다:
$\min_{\mathbf{z}_i} \sum_i \left\| \mathbf{z}_i - \sum_{j \in \mathcal{N}(i)} w_{ij} \mathbf{z}_j \right\|^2$
8.6 다른 차원 축소 기법
| 차원 축소 기법 | 유형 | 목적 | 설명 | 특징 |
| MDS (Multidimensional Scaling) |
비선형 | 거리 보존 |
샘플 간의 유클리디언 거리(또는 지정된 거리 행렬)를 저차원에서 최대한 유지 | 전역 거리 구조 보존 전체 분포 시각화 |
| Isomap | 비선형 | 매니폴드 보존 | 고차원 공간에서 이웃 그래프 구성 → 지오데식 거리 계산 → MDS 적용 | 곡면 위의 구조를 유지 MDS 개선형 |
| t-SNE (t-Distributed Stochastic Neighbor Embedding) |
비선형 | 시각화 | 고차원과 저차원 모두에서 샘플 간 확률 기반 유사도를 정의하고, 이를 최소화 | 국소 구조에 매우 민감 시각화 탁월 (클러스터링 명확) |
| LDA (Linear Discriminant Analysis) |
선형 | 분류 | 클래스 간 분산은 최대화, 클래스 내 분산은 최소화하는 투영 방향 찾기 | 지도 학습 기반 클래스 레이블 필요, 분류 성능 강화 |
from sklearn.manifold import MDS, Isomap, TSNE
from sklearn.datasets import make_swiss_roll
X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
mds = MDS(n_components=2, normalized_stress=False, random_state=42)
X_reduced_mds = mds.fit_transform(X_swiss)
isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X_swiss)
tsne = TSNE(n_components=2, init="random", learning_rate="auto",
random_state=42)
X_reduced_tsne = tsne.fit_transform(X_swiss)
titles = ["MDS", "Isomap", "t-SNE"]
plt.figure(figsize=(11, 4))
for subplot, title, X_reduced in zip((131, 132, 133), titles,
(X_reduced_mds, X_reduced_isomap, X_reduced_tsne)):
plt.subplot(subplot)
plt.title(title)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t )
plt.xlabel("$z_1$")
if subplot == 131:
plt.ylabel("$z_2$", rotation=0)
plt.grid(True)
plt.show()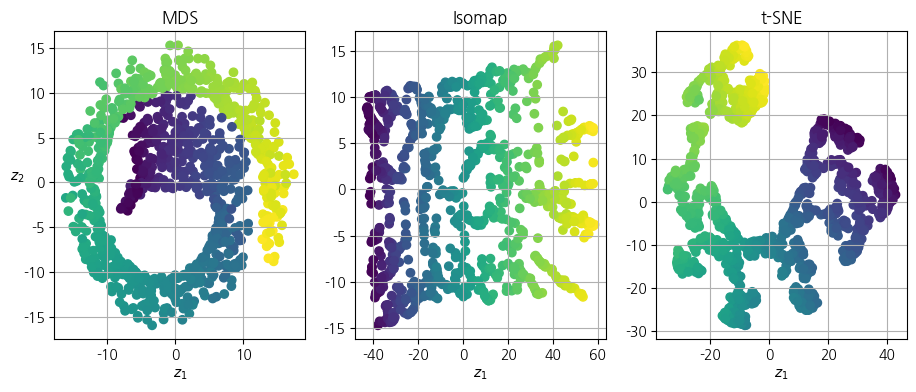
- 스위스롤 차원 축소 코드의 실행 결과입니다. 결과는 아래와 같습니다.
- MDS는 전체 거리 유지에 충실하지만, 스위스롤과 같은 비선형 구조에는 한계가 있습니다.
- Isomap은 매니폴드 구조를 어느 정도 잘 펼칩니다.
- t-SNE는 국소적인 구조나 클러스터 구분이 명확해 시각화에 매우 유용하지만, 전체적인 전역 구조는 왜곡될 수 있습니다.