4. 강화학습 - Q-Network
Q-Network의 등장배경
Q-Learning은 (Q(s, a))을 학습하여 Q-table 를 이용해 최적의 정책을 찾는 강화학습 알고리즘입니다.

전통적인 Q-Learning은 작은 Q-Table 공간에서는 잘 작동하지만, Q-Table 공간이 매우 크거나 연속적일 경우 Q-값을 테이블 형태로 저장하는 것은 불가능합니다. 머신러닝을 생각하면, 동일 state 즉 row의 데이터가 중복되는 경우는 거의 없습니다. 실제, 세계에서는 Q-Table로 강화학습이 거의 불가능합니다. 따라서 Q함수를 근사하기 위해 Q-함수 근사 방법(Q-Function Approximation)으로 신경망(Neural Network)을 활용한 것이 Q-Network입니다.

이 그림은 Q-Network의 구조를 시각적으로 나타낸 것입니다.
Q-Network는 Q-함수와 유사하게, state와 action을 입력으로 받아 딥러닝 모델을 통해 학습되며, 그 출력으로 예상되는 reward 값을 제공합니다.

또는, 입력으로 state만을 사용하고 출력으로는 모든 가능한 action에 대한 Q-값을 계산하여 제공할 수도 있습니다.

일반적으로, Q-Network는 두 번째 방식, 즉 상태 를 입력으로 받아 모든 가능한 행동 a에 대한 모든 Q-값 Q(s,a)를 출력합니다.
Q-Network는 Q-Function을 근사합니다. 이는 강화학습에서 상태-행동 가치 함수 Q(s,a)를 신경망으로 모델링한 것입니다.
Q-Network에서는 입력값 x, 예측값 y_pred, 목표값 y_true, 그리고 손실 함수 L를 정의해야 합니다. 이로 인해 Q-Network의 학습 과정은 일반적인 딥러닝 모델과 유사하지만, 입출력 정의와 목표값 설정 방식이 강화학습의 핵심입니다.
Q-Learning의 핵심 수식
1.결정론적 수식 (Deterministic): 미래 상태 s′에서 가능한 행동 a′의 최대 Q-값을 반영하여 현재 상태 s에서의 Q-값을 업데이트합니다.

2. 확률론적 수식 (Stochastic) : 행동 정책 π를 통해 확률적으로 미래의 Q-값을 계산합니다.

Q-Network에서는 첫 번째 결정론적 수식을 사용합니다. 딥 Q-learning의 학습률은 딥러닝 모델 내부에서 자동으로 가중치 업데이트 과정에서 반영되기 때문에 별로로 사용할 필요가 없습니다.
- 입력(Input): 인공신경망의 입력 x는 현재 상태 s 사용합니다.(보통 벡터 형태로 표현).
- 출력(Output): y_pred 딥러닝에서 예측한 가능한 모든 행동 a의 Q-값 Q(s,a)을 사용합니다.
- 목표(Target, Label): y_true는 Q-Learning의 업데이트 식에 따라, 목표 Q-값(Target Q-value)을 설정합니다.

Q알고리즘의 예측값과 실제 값은 아래와 같이 표현할 수 있습니다.

손실 함수(Loss Function): 결국 손실함수는 y_true와 y_pred의 차이로 정의할 수 있습니다.
는 신경망의 가중치입니다. 손실 함수를 최소화하면서 Q-Network를 학습합니다.

여기까지 정의하면, 강화학습 문제는 일반 딥러닝 모델과 구조적으로 유사집니다.
Q-Network의 알고리즘은 아래와 같이 표현됩니다.

Frozen lake Q-Network작성
%%time
import numpy as np
import gym
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# FrozenLake 환경 생성
env = gym.make("FrozenLake-v1", is_slippery=False, render_mode=None)
# 하이퍼파라미터 설정
state_size = env.observation_space.n
action_size = env.action_space.n
hidden_size = 16
learning_rate = 0.001
gamma = 0.99 # 할인율
epsilon = 1.0 # 탐험 확률 초기값
epsilon_decay = 0.99 # 탐험 확률 감소율
epsilon_min = 0.1 # 탐험 확률 최소값
episodes = 2000 # 에피소드 수
# Q-Network 정의
class QNetwork(nn.Module):
def __init__(self, state_size, hidden_size, action_size):
super().__init__()
self.fc1 = nn.Linear(state_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, action_size)
def forward(self, x):
x = torch.relu(self.fc1(x))
return self.fc2(x)
# Q-Network 및 Optimizer 초기화
model = QNetwork(state_size, hidden_size, action_size)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# SmoothL1Loss는 MSELoss와 L1Loss(Mean Absolute Error)의 장점을 결합한 손실 함수
# 오차가 작을 때는 MSE처럼 작동, 오차가 클 때는 MAE처럼 작동하여 이상값의 영향을 줄임
criterion = nn.SmoothL1Loss()
# 미리 생성된 One-Hot 벡터
# state가 숫자 크기와 관계 없이 이산 데이터임으로 onehot으로 입력합니다.
states = torch.eye(state_size, dtype=torch.float32)
# 에피소드 별 총 보상 저장 리스트
rewards = []
init_state = True
# 학습 루프
for episode in range(episodes):
# Step 1: 환경 초기화 및 상태 가져오기
state, _ = env.reset()
total_reward = 0
done = False
while not done:
# Step 2: epsilon-greedy 정책으로 행동 선택
# Q(s,a) → 현재 상태 𝑠에서의 Q-값 배열.
current_q_values = model(states[state].unsqueeze(0))
if (np.random.rand() < epsilon) or init_state:
action = env.action_space.sample() # 탐험
else:
action = current_q_values.argmax().item() # 활용
# Step 3: 행동 수행 및 새로운 상태와 보상 관찰
new_state, reward, terminated, truncated, info = env.step(action)
if init_state and (reward > 0):
init_state = False
# Step 4: 목표 Q값 계산
target_q_values = current_q_values.clone().detach()
if terminated:
target_q_values[0, action] = reward
else:
# next_q_values: 𝑄(𝑠′,𝑎′ ) → 다음 상태 𝑠′에서의 Q-값 배열.
next_q_values = model(states[new_state].unsqueeze(0)) # 다음 상태의 Q-값
# max_next_q_value: max 𝑄(𝑠′,𝑎′) → 다음 상태에서 최댓값
max_next_q_value = next_q_values.max(1)[0].item() # 활용
target_q_values[0, action] = reward + gamma * max_next_q_value
# Step 5: 모델 업데이트
loss = criterion(current_q_values, target_q_values)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_reward += reward # 보상 누적
state = new_state # 다음 상태로 이동
done = terminated or truncated
epsilon = max(epsilon_min, epsilon*epsilon_decay) # 탐험 확률 감소
rewards.append(total_reward) # 에피소드 별 총 보상 저장
# 결과 출력
print("성공률 :", sum(rewards) / episodes)
plt.bar(range(len(rewards)), rewards, color="blue")
plt.show()성공률 : 0.784
Q learning의 Q테이블을 사용했을 때 보다 성능이 약간 떨어집니다.
Q함수의 근사라서 Q테이블보다는 떨어지는 것이 당연할것 같습니다.
다음은 조금더 복잡한 CartPole로 작성합니다.
CartPole은 강화학습 알고리즘(예: Q-Learning, Deep Q-Network, Policy Gradient 등)을 학습하고 테스트하는 데 주로 사용됩니다.
CartPole 문제는 막대(Pole)를 수평으로 움직이는 카트(Cart)에 세운 상태에서, 막대가 넘어지지 않도록 카트를 좌우로 움직이는 문제입니다.
상태는 카트의 수평 위치, 카트의 수평 이동 속도, 막대의 기울어진 각도, 막대가 회전하는 속도, 4가지 연속적인 변수로 표현됩니다. Action은 0 왼쪽, 1 오른쪽으로 이동 두가지 값으로 구성됩니다. 매 타임 스텝마다 +1점을 보상받습니다.
CartPole 환경은 상태 공간이 연속적인 값들(카트 위치, 속도, 막대 각도, 각속도)로 이루어져 있기 때문에, Q-테이블 방식(Q-Learning의 기본 구현)은 현실적으로 사용할 수 없습니다.
코드구현
%%time
import numpy as np
import gym
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# CartPole 환경 생성
env = gym.make("CartPole-v1", render_mode="human")
# 하이퍼파라미터 설정
state_size = env.observation_space.shape[0] # 상태 차원 (연속형)
action_size = env.action_space.n # 행동 차원 (이산형)
hidden_size = 24 # 은닉층 크기
learning_rate = 0.1
gamma = 0.9 # 할인율
epsilon = 1.0 # 탐험 확률 초기값
epsilon_decay = 0.995 # 탐험 확률 감소율
epsilon_min = 0.1 # 탐험 확률 최소값
episodes = 2000 # 에피소드 수
max_steps =10000 # 에피소드 당 최대 스텝 수
# Q-Network 정의
class QNetwork(nn.Module):
def __init__(self, state_size, hidden_size, action_size):
super().__init__()
self.fc1 = nn.Linear(state_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, action_size)
def forward(self, x):
x = torch.relu(self.fc1(x))
return self.fc2(x)
# Q-Network 및 Optimizer 초기화
model = QNetwork(state_size, hidden_size, action_size)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.SmoothL1Loss()
# 학습 루프
rewards = []
for episode in range(episodes):
state, _ = env.reset() # 환경 초기화
state = torch.tensor(state, dtype=torch.float32)
total_reward = 0
for step in range(max_steps):
# Step 1: epsilon-greedy 정책으로 행동 선택
if np.random.rand() < epsilon:
action = env.action_space.sample() # 탐험
else:
q_values = model(state.unsqueeze(0))
action = q_values.argmax().item() # 활용
# Step 2: 행동 수행 및 새로운 상태와 보상 관찰
new_state, reward, terminated, truncated, _ = env.step(action)
new_state = torch.tensor(new_state, dtype=torch.float32)
if terminated:
reward = 0
done = terminated or truncated
# Step 3: 목표 Q값 계산
current_q_values = model(state.unsqueeze(0))
target_q_values = current_q_values.clone().detach()
if done:
target_q_values[0, action] = reward
else:
next_q_values = model(new_state.unsqueeze(0))
max_next_q_value = next_q_values.max(1)[0].item()
target_q_values[0, action] = reward + gamma * max_next_q_value
# Step 4: 모델 업데이트
loss = criterion(current_q_values, target_q_values)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_reward += reward
state = new_state
if done:
break
# 탐험 확률 감소
epsilon = max(epsilon_min, epsilon * epsilon_decay)
rewards.append(total_reward)
# 진행 상태 출력
print(f"Episode: {episode + 1}, Reward: {total_reward}")
# 결과 출력
print("평균 보상:", np.mean(rewards))
plt.plot(rewards)
plt.xlabel("Episode")
plt.ylabel("Reward")
plt.title("CartPole Rewards")
plt.show()
# 환경 종료
env.close()평균 보상: 12.506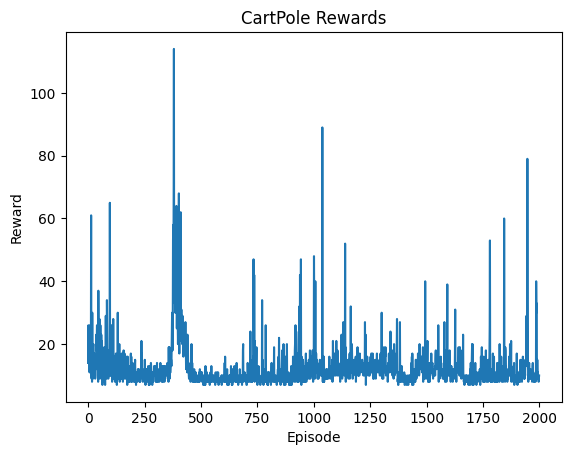
간단한 모델에서는 성능이 좋았지만, 평균 보상 12.5로 성능이 좋지 못합니다.
강화학습에, 인공신경망을 적용하는 기술은 예전에도 있었지만 이러한 문제로 많이 사용되지 못했습니다.
이러한 문제를 해결한 것이 2013년 2015년 딥마인드의 네이쳐 논문이었습니다.
Q-Network의 어떤 문제가 있는지, 딥마인드에서 어떤 알고리즘으로 문제를 해결했는지 다음글에서 알아보겠습니다.