Graph Neural Networks: A Review of Methods and Applications
논문 제목: Graph Neural Networks: A Review of Methods and Applications
주제: 이 논문에서는 GNN을 모델 유형, 그래프 유형, 학습 방식, 연산 모듈 등 다양한 기준으로 분류하였으며, 각각의 분류에 맞는 대표적인 연구들을 정리하였습니다.
발행 연도: 2018-2021(v6)
https://arxiv.org/abs/1812.08434
논문 요약
GNN 모델 설계의 일반적인 절차를 소개합니다.
일반적으로 GNN을 설계는 4단계로 구성되며, 각 단계는 그래프 구조와 문제 유형에 따라 다르게 적용됩니다.
GNN 모델 설계의 4단계
1. 그래프 구조 찾기 (Find Graph Structure)
1) 구조적 시나리오 (Structural Scenarios)
그래프가 명시적으로 존재하는 경우입니다. 주어진 그래프 구조를 그대로 사용할 수 있습니다.
예: 분자 구조 분석, 물리 시스템 모델링, 지식 그래프, 소셜 네트워크 등
2) 비구조적 시나리오 (Non-Structural Scenarios)
그래프가 암묵적으로 존재하는 경우입니다.
텍스트, 이미지, 비정형 데이터에서 그래프를 새로 구축해야 합니다.
노드 및 엣지를 정의하여 의미 있는 그래프를 만들어야 합니다.
예: Dependency Tree, Scene Graph
2. 그래프 유형 및 크기 결정 (Specify Graph Type and Scale)
1) 그래프 유형 (Graph Type)
. 방향성 (Directed / Undirected)
. 동형 / 비동형 그래프 (Homogeneous / Heterogeneous)
. 정적 / 동적 그래프 (Static / Dynamic)
2) 그래프 크기 (Graph Scale)
. 소규모 그래프(Small-scale Graph):
그래프의 인접 행렬(Adjacency Matrix) 또는 라플라시안 행렬(Laplacian Matrix)을 메모리에 저장할 수 있음.
일반적인 GNN 모델 (GCN, GAT 등) 적용 가능.
. 대규모 그래프(Large-scale Graph):
전체 인접 행렬을 저장하기 어렵고, 연산 비용이 큼.
샘플링 기반 GNN (GraphSAGE, FastGCN, ClusterGCN).
3. 손실 함수 설계 (Design Loss Function)
일반적으로 GNN은 노드 수준, 엣지 수준, 그래프 수준의 작업을 수행할 수 있습니다.
1) 작업 유형에 따른 손실 함수
(1) 노드 레벨(Node-Level Tasks)
. 노드 분류(Node Classification): 각 노드를 특정 클래스로 분류(손실 함수: Cross-Entropy Loss)
. 노드 회귀(Node Regression): 연속적인 값을 예측하는 문제
. 노드 클러스터링(Node Clustering): 비슷한 노드를 그룹화하는 문제
(2) 엣지 레벨(Edge-Level Tasks)
. 링크 예측(Link Prediction): 두 노드 간 연결 가능성을 예측
예: 소셜 네트워크에서 친구 추천
. 엣지 분류(Edge Classification): 엣지 유형을 분류하는 문제
(3) 그래프 레벨 (Graph-Level Tasks)
. 그래프 분류(Graph Classification): 그래프 전체를 하나의 클래스로 분류
. 그래프 회귀(Graph Regression): 그래프 속성을 예측
2) 학습 방식에 따른 손실 함수
(1) 지도 학습(Supervised Learning)
(2) 반지도 학습(Semi-Supervised Learning)
(3) 비지도 학습(Unsupervised Learning)
4. 계산 모듈을 사용하여 모델 구축 (Build Model using Computational Modules)
GNN 모델을 구축할 때 필요한 계산 모듈을 결정합니다.
1) 전파 모듈 (Propagation Module): 메시지 전달 및 정보 집계 수행
예: GCNConv, GATConv, SAGEConv
2) 샘플링 모듈 (Sampling Module): 대규모 그래프에서 효율적인 학습 수행
예: GraphSAGE, FastGCN, ClusterGCN
3) 풀링 모듈 (Pooling Module): 그래프 구조를 계층적으로 표현
예: DiffPool, SAGPool

GNN의 연산 모듈 구현 (Instantiations of Computational Modules)
GNN 모델은 여러 계산 모듈(Computational Modules)로 구성되며, 이 모듈들은 메시지 전달(Message Passing) 및 학습 과정에서 중요한 역할을 합니다.
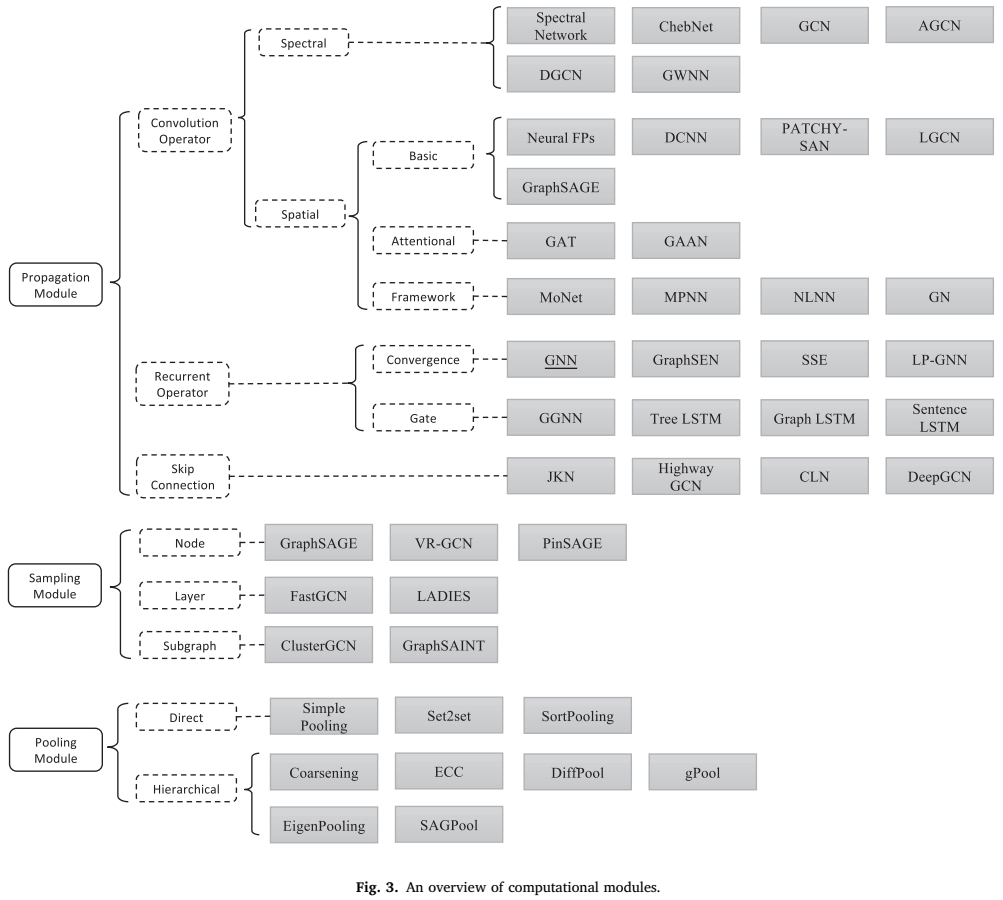
1. 전파 모듈 (Propagation Modules)
그래프 내에서 정보를 전달하는 역할을 수행하는 핵심 모듈입니다.
(1) 합성곱 연산자 (Convolution Operator)
그래프 데이터에서 CNN을 적용하기 위해 개발된 다양한 그래프 합성곱(GCN, Graph Convolution) 방법이 존재합니다.
합성곱 방식은 크게 스펙트럴(Spectral) 접근법과 공간(Spatial) 접근법으로 구분됩니다.
① 스펙트럴(Spectral) 접근법
그래프 신호 처리(Graph Signal Processing) 개념을 이용하여, 푸리에 변환을 기반으로 그래프의 합성곱 연산을 정의합니다.
그래프 라플라시안(Laplacian) 행렬을 이용하여 노드 간 신호를 주파수 도메인에서 변환하고 필터링합니다.
주요 모델 : ChebNet (2016), GCN (Kipf & Welling, 2017)
② 공간(Spatial) 접근법
공간 기반 방법은 CNN의 지역 연산(Local Operation) 개념을 그래프에 적용한 방식입니다.공간 기반 방법은 CNN의 지역 연산(Local Operation) 개념을 그래프에 적용한 방식입니다.
직접 노드의 이웃을 탐색하면서 메시지를 전달하는 방식입니다.
주요 모델 : GraphSAGE (Hamilton et al., 2017), GAT (Graph Attention Network, 2018)
(2) 순환 연산자 (Recurrent Operator)
그래프에서 노드 간 정보가 순차적으로 전달될 경우, RNN 기반의 순환 구조를 도입할 수 있습니다.
① 재귀형 그래프 신경망 (Recursive GNN)
초기 연구로 순환 신경망(RNN)을 그래프에 적용한 방법입니다.
주요 모델 : GGNN (Gated Graph Neural Network, 2015), Graph LSTM
(3) 스킵 연결 (Skip Connection)
Deep GNN 모델에서 과적합(Overfitting)과 과평활화(Over-smoothing) 문제를 해결하기 위해 스킵 연결(Skip Connection)을 추가합니다.
주요 모델 : Highway GCN (2018), Jump Knowledge Network (JKN, 2018), DeepGCNs (2019)
2. 샘플링 모듈 (Sampling Modules)
대규모 그래프에서는 모든 이웃 노드를 탐색하는 것이 비효율적이므로, 샘플링 기법을 활용하여 그래프를 효율적으로 학습합니다.
(1) 노드 샘플링 (Node Sampling)
. GraphSAGE (Hamilton et al., 2017):일정 개수의 이웃 노드만 샘플링하여 학습.
. PinSAGE (Ying et al., 2018): 중요도가 높은 노드만 샘플링
(2) 레이어 샘플링 (Layer Sampling)
. FastGCN (Chen et al., 2018): 각 레이어에서 중요도가 높은 노드를 샘플링
. LADIES (Zou et al., 2019): 이웃 노드를 한 번에 샘플링하여 레이어를 구성
3. 풀링 모듈 (Pooling Modules)
CNN에서 사용되는 것처럼, Pooling을 이용하여 그래프에서도 중요한 정보를 추출하고 차원을 축소하는 역할을 합니다.
계층적 그래프 표현 학습하여 래프 내 고차원 정보를 요약하여 더 좋은 표현 학습이 가능합니다.
(1) 직접 풀링 (Direct Pooling)
Set2Set (Vinyals et al., 2015): LSTM을 활용한 집계 함수.
SortPooling (Zhang et al., 2018): 노드들을 정렬하여 CNN에 적용.
(2) 계층적 풀링 (Hierarchical Pooling)
DiffPool (Ying et al., 2018): 학습 가능한 계층적 클러스터링 적용
gPool (Gao & Ji, 2019): 노드 중요도 기반 선택.
SAGPool (Lee et al., 2019): Self-Attention 기반 풀링 적용

4. 그래프 유형과 크기를 고려한 GNN 변형 모델 (Variants Considering Graph Type and Scale)
그래프의 유형(Graph Type)과 크기(Scale) 에 따라 GNN 모델이 어떻게 설계되고 변형되는지를 설명합니다.
4.1 그래프 유형(Graph Type)에 따른 변형
그래프는 크게 동형 그래프(Homogeneous Graph) 와 비동형 그래프(Heterogeneous Graph) 로 구분됩니다.
1) 동질 그래프 (Homogeneous Graph) : 모든 노드와 엣지가 동일한 타입을 가지는 그래프.
일반적인 GCN, GAT, GraphSAGE 등의 모델이 사용됨.
예: 논문 인용 네트워크, 소셜 네트워크.
2) 비동형 그래프 (Heterogeneous Graph) : 노드와 엣지가 여러 개의 타입을 가지는 그래프.
비동형 그래프에서는 일반적인 GNN 모델을 직접 적용하기 어려우므로, 비동형 그래프를 위한 변형 모델이 필요합니다.
. HAN (Heterogeneous Graph Attention Network, 2019):각 노드 타입별로 Attention 메커니즘을 적용하여 가중치를 학습.
. MAGNN (Meta-path Aggregated Graph Neural Network, 2020) : 메타패스(Meta-path)를 활용하여 그래프 구조를 반영한 GNN 모델.
4.2 그래프 크기(Scale)에 따른 변형
그래프가 커질수록 메모리와 연산량이 기하급수적으로 증가하기 때문에, 대규모 그래프를 처리하기 위한 GNN 변형 기법이 필요합니다.
1) 대규모 그래프를 위한 GNN 모델
일반적인 GCN은 그래프 전체를 메모리에 로드하여 학습하기 때문에, 대규모 그래프에서는 비효율적입니다.
이를 해결하기 위해 샘플링(Sampling) 기법과 분할(Partitioning) 기법이 등장했습니다.
(1) 샘플링 기반 GNN
이웃 노드가 많을 경우, 모든 노드를 탐색하는 것이 비효율적이므로, 일부 노드만 샘플링하여 학습하는 기법입니다.
. GraphSAGE (2017) : 샘플링된 이웃 노드를 평균(Aggregation)하여 노드 표현 학습.
. FastGCN (2018) : 레이어별로 샘플링하여 연산 속도를 향상.
. LADIES (2019) : 중요도가 높은 노드를 선택적으로 샘플링.
(2) 서브그래프 기반 GNN
그래프를 여러 개의 작은 그래프로 분할하여 학습하는 방식입니다.
. ClusterGCN (2019) : 그래프를 클러스터링하여 작은 그래프 단위로 학습.
. GraphSAINT (2020) : 확률적 샘플링 기법을 사용하여 대규모 그래프를 처리.
4.4 기타 그래프 유형 (Other Graph Types)
(1) 하이퍼그래프 (Hypergraph) :
기존 그래프는 두 노드 간의 관계(Edge)를 1:1 연결하는 구조입니다.
하지만 하이퍼그래프(Hypergraph)는 한 개의 엣지가 여러 개의 노드를 동시에 연결할 수 있습니다.
. 하이퍼그래프의 예시
논문-저자 네트워크: 한 개의 논문(Paper)은 여러 명의 저자(Author)와 연결됨.
전자상거래 추천 시스템: 한 개의 상품(Product)은 여러 개의 카테고리(Category)와 동시에 연결될 수 있음.
단백질 네트워크: 하나의 단백질이 여러 개의 생화학적 반응과 연관될 수 있음.
. 하이퍼그래프 GNN 모델
HGNN (Hypergraph Neural Network, Feng et al., 2019)
기존의 GCN을 하이퍼그래프 구조에 맞게 변형.
하이퍼엣지(Hyperedge)를 통해 여러 개의 노드 간 정보를 공유.
HyperGAT (Hypergraph Attention Network, 2020)
하이퍼그래프에서 Attention Mechanism을 적용하여 노드 간 관계를 학습.
(2) 동적 그래프 (Dynamic Graph)
일반적인 그래프는 정적인 구조(Static Graph)를 가정하지만, 시간이 지남에 따라 변화하는 그래프(Dynamic Graph)가 존재합니다.
예를 들어:
소셜 네트워크에서 사용자 간의 관계 변화 (새로운 친구 추가, 관계 단절)
금융 거래 네트워크에서 트랜잭션 흐름 변화
교통 네트워크에서 실시간 교통량 변화
. 동적 그래프의 유형
- 연속적인 변화 (Continuous-time Dynamic Graph)
엣지와 노드가 이벤트 기반(Event-based)으로 발생하며, 연속적인 시간 축을 가짐.
예: 금융 거래 네트워크 (새로운 결제, 송금 발생)
- 불연속적인 변화 (Discrete-time Dynamic Graph)
일정한 시간 간격(예: 1시간, 1일)으로 그래프를 업데이트함.
예: 소셜 네트워크에서 매일 사용자 간의 관계 변화 추적
. 동적 그래프 GNN 모델 : EvolveGCN (Pareja et al., 2020), TGAT (Temporal Graph Attention Network, 2020)
(3) 지식 그래프 (Knowledge Graph)
객체(Entities)와 관계(Relations)를 그래프 구조로 표현한 것.
예: 위키피디아 지식 그래프, 구글 지식 그래프
지식 그래프 GNN 모델 :
R-GCN (Relational Graph Convolutional Network, 2018) : 다양한 관계(Relation)를 고려하여 다중 유형의 엣지(Multi-relational Edges)를 학습.
KBGAT (Knowledge Base GAT, 2019) : GAT 기반으로 지식 그래프에서 중요 노드에 주의(attention)를 부여하는 기법.
(4) 지오메트릭 그래프 (Geometric Graph)
그래프의 노드가 공간적 좌표(Spatial Coordinates)를 가지는 경우.
예: 자율 주행, 3D 물체 인식, 단백질 구조 분석
지오메트릭 그래프 GNN 모델 :
MoNet (Monti et al., 2017) : CNN의 합성곱 필터를 지오메트릭 그래프(Geometric Graph)에 적용하는 방법.
PointNet (Qi et al., 2017) : 3D 점군 데이터(Point Cloud)를 처리하는 모델.
Geo-GNN (Geometric Graph Neural Network, 2020) : 그래프의 공간적 특성을 반영한 GNN 모델.
5. GNN의 주요 응용 분야 (Applications of GNNs)
GNN은 다양한 산업과 연구 분야에서 활용됩니다. 이 장에서는 GNN이 적용되는 대표적인 응용 사례를 살펴봅니다.
5.1 노드 수준(Task at Node Level) 응용
노드 수준의 작업에서는 개별 노드에 대한 정보를 예측하는 것이 목표입니다.
1) 노드 분류 (Node Classification)
그래프의 각 노드가 특정 클래스로 분류되는 작업입니다.
예: 소셜 네트워크에서 사용자의 관심사를 분류, 논문 인용 네트워크에서 논문의 주제 분류
대표적인 데이터셋:Cora, Citeseer, PubMed
적용 모델 : GCN (Kipf & Welling, 2017),GAT (Graph Attention Network, 2018),GraphSAGE (Hamilton et al., 2017)
2) 링크 예측 (Link Prediction)
그래프 내에서 연결되지 않은 두 노드가 연결될 확률을 예측하는 작업.
예: 소셜 네트워크에서 친구 추천, 논문 추천 시스템
적용 모델 : VGAE (Variational Graph Autoencoder, 2016), SEAL (Subgraph Embedding-based Link Prediction, 2018)
5.2 그래프 수준(Task at Graph Level) 응용
그래프 전체를 하나의 단위로 보고 분석하는 작업.
1) 화합물 속성 예측 (Molecular Property Prediction)
화학 분자의 구조를 그래프로 표현하여 분자의 특성을 예측.
예: 신약 개발, 단백질 상호작용 분석
대표적인 데이터셋: QM9 (화합물 데이터셋), MUTAG (발암성 화합물 데이터셋)
적용 모델 : GCN,GIN (Graph Isomorphism Network, 2019),GraphSAGE
2) 그래프 분류 (Graph Classification)
그래프 전체를 하나의 클래스로 분류하는 작업.
예: 소셜 네트워크에서 사용자 그룹 분류, 단백질 구조 분류
대표적인 데이터셋:TUDataset (소셜 네트워크 및 단백질 구조 데이터)
적용 모델 : DiffPool (Hierarchical Graph Pooling, 2018), Graph U-Net (2019)
5.3 시공간 그래프 (Spatial-Temporal Graph) 응용
시간에 따라 변화하는 그래프를 모델링하는 작업.
1) 교통 예측 (Traffic Forecasting)
도로망을 그래프로 표현하여 차량 흐름을 예측.
예: Google Maps, Waze의 실시간 교통 예측
적용 모델: DCRNN (Diffusion Convolutional Recurrent Neural Network, 2018), ST-GCN (Spatial-Temporal Graph Convolutional Networks, 2018)
2) 금융 및 사기 탐지 (Fraud Detection)
금융 거래 네트워크에서 이상 패턴을 탐지하여 사기를 예측.
적용 모델: GCN 기반 사기 탐지 모델
7. GNN 분석 (Analyses of GNNs)
이 장에서는 GNN의 이론적 및 실험적 분석을 다룹니다.
GNN이 어떻게 동작하는지, 그리고 모델의 일반화 성능, 표현력, 변이성, 전이성 등을 설명하는 연구를 요약합니다.
7.1 이론적 분석 (Theoretical Aspect)
7.1.1 그래프 신호 처리 (Graph Signal Processing)
스펙트럼(Spectral) 관점에서 보면, GCN은 그래프의 신호 처리 이론을 따르며, 주어진 특징을 스펙트럼 도메인에서 변환 후 합성곱 연산을 수행합니다.
Li et al. (2018) 연구에 따르면, GCN의 합성곱 연산은 사실상 라플라시안 스무딩(Laplacian Smoothing)으로 작용하여 인접한 노드들이 비슷한 특성을 가지도록 만듦.
SGC(Wu et al., 2019)는 레이어 사이의 가중 행렬과 비선형성을 제거하여, 저역 통과 필터(Low-pass Filter)가 GNN이 작동하는 핵심 원리임을 증명.
GNN의 스펙트럴 분석은 GCN이 그래프 구조를 통해 정보를 평활화(Smoothing)하는 과정임을 증명함.
추가 연구
AGC (Zhang et al., 2019) → 주파수 응답 함수를 기반으로 새로운 그래프 필터 설계.
AGE (Cui et al., 2020) → 최대 고유값(λmax)을 활용한 최적 필터 제안.
GraphHeat (Xu et al., 2019) → 히트 커널(Heat Kernel)을 활용하여 저역 통과 필터링 성능 개선.
7.1.2 일반화 성능 (Generalization)
GNN의 일반화 성능은 필터의 특성 및 그래프 구조의 노이즈 정도에 의해 결정됨.
Scarselli et al. (2018)은 특정 GNN 모델들의 VC 차원(VC-Dimension)을 분석하여 일반화 성능을 수학적으로 입증.
Garg et al. (2020)은 신경망의 라데마허 경계(Rademacher Bounds)를 활용한 일반화 성능 개선 연구 수행.
Verma & Zhang (2019) → GCN의 안정성과 일반화 성능이 필터의 최대 고유값에 의해 결정됨을 입증.
Knyazev et al. (2019) → GAT(GATConv)가 주의 메커니즘을 통해 노이즈가 많은 그래프에서도 일반화 가능함을 증명.
7.1.3 표현력 (Expressivity)
GCN, GraphSAGE 모델은 구조적 분별력(Structural Discriminative Power)이 제한적임이 연구를 통해 밝혀짐.
GNN은 구조적으로 유사한 그래프를 구별하는 능력이 제한적이므로, 이를 해결하기 위한 WL 기반 개선 모델(GIN 등)이 필요.
Weisfeiler-Leman(WL) 테스트: GIN(Graph Isomorphism Network, Xu et al., 2019)은 WL 테스트를 기반으로 GNN의 표현력을 향상.
Garg et al. (2020)는 GNN이 글로벌 그래프 속성을 학습하기 어렵다는 한계를 지적.
7.1.4 변이성 (Invariance)
그래프 데이터는 노드 순서가 없기 때문에, GNN 출력이 순열 불변(Permutation-Invariant)해야 함.
GNN은 입력 그래프의 순열 변화에도 불변한 표현을 학습해야 하며, 이를 보장하기 위한 새로운 아키텍처 연구가 필요.
Maron et al. (2019) → 불변 선형층을 사용하여 GNN의 순열 불변성을 보장하는 방법 제안.
Chen et al. (2019) → 그래프 동형성(Graph Isomorphism) 테스트와 GNN의 표현력 관계 연구.
7.1.5 전이 학습 성능 (Transferability)
GNN이 한 그래프에서 학습된 모델을 다른 그래프에 적용할 수 있는가?
GNN은 같은 구조를 가진 그래프에서는 전이 학습이 가능하지만, 서로 다른 구조에서는 일반화 성능이 낮아질 수 있음.
→ Levie et al. (2019) 연구: GNN의 스펙트럼 필터는 같은 도메인 내 그래프에서는 전이 가능.
→ Ruiz et al. (2020) 연구: 그래프온(Graphon) 개념을 활용하여 GNN의 전이 학습 성능 평가.
7.1.6 라벨 효율성 (Label Efficiency)
지도 학습 기반 GNN은 많은 레이블이 필요하지만, 적은 라벨로도 학습 성능을 높이는 방법이 연구됨.
능동 학습 기법을 활용하면 소량의 레이블 데이터만으로도 GNN 학습 성능을 극대화 가능.
능동 학습(Active Learning) 기법 활용:
Gao et al. (2018), Hu et al. (2020) → 정보량이 많은 노드(고차수 노드, 불확실성이 높은 노드)만 선택하여 학습 효율 향상.
7.2 실험적 분석 (Empirical Aspect)
7.2.1 평가 (Evaluation)
GNN 모델의 공정한 평가를 위한 연구가 필요.
GNN 연구에서는 실험 조건을 표준화하고, 데이터셋 분할 및 평가 기준을 통일하는 것이 중요.
Shchur et al. (2018) → GNN 모델을 동일한 데이터셋 분할 방식과 하이퍼파라미터 튜닝 방식으로 비교하여 성능 평가.
실험의 재현 가능성(Reproducibility) 문제 제기 : 동일한 실험 조건에서도 데이터셋 분할 방식에 따라 성능 차이가 발생할 수 있음.
7.2.2 벤치마크 (Benchmarks)
GNN 연구의 성능 비교를 위한 표준 벤치마크 데이터셋이 필요.
GNN의 성능을 평가하기 위해서는 표준화된 벤치마크 데이터셋이 필요하며, Open Graph Benchmark(OGB) 등이 이에 활용될 수 있음.
Open Graph Benchmark(OGB) → 대규모 그래프 데이터셋 및 공정한 비교 프레임워크 제공.
Benchmark 관련 연구: Hu et al. (2020) → GNN 성능 평가를 위한 공정한 벤치마크 데이터셋 제안.
8. GNN의 응용 (Applications of GNNs)
GNN은 지도 학습(Supervised), 반지도 학습(Semi-Supervised), 비지도 학습(Unsupervised), 강화 학습(Reinforcement Learning) 등 다양한 학습 방식에서 활용됩니다.
이 장에서는 GNN의 주요 응용 사례를 두 가지 범주로 분류하여 설명합니다.
(1) 구조적 시나리오 (Structural Scenarios) : 데이터가 명확한 관계 구조를 가지는 경우.
예: 그래프 마이닝, 물리 시스템 모델링, 화학 시스템, 지식 그래프, 교통 네트워크, 추천 시스템.
(2) 비구조적 시나리오 (Non-Structural Scenarios) : 데이터 간 관계 구조가 명확하지 않은 경우.
예: 이미지 처리(Computer Vision), 자연어 처리(Natural Language Processing, NLP).
8.1 구조적 시나리오 (Structural Scenarios)
그래프 형태로 데이터를 표현할 수 있는 분야에서 GNN이 활용됩니다.
8.1.1 그래프 마이닝 (Graph Mining)
그래프 데이터에서 패턴을 찾거나 분석하는 작업을 포함합니다.
① 그래프 매칭 (Graph Matching) : 그래프 간 유사성을 찾는 작업.
예: 화합물 구조 비교, 유전자 네트워크 분석.
대표 모델: Siamese MPNN (Riba et al., 2018), GCN 기반 매칭 (Li et al., 2019b).
② 그래프 군집화 (Graph Clustering)
그래프 내 노드를 그룹화하는 작업.
예: 소셜 네트워크에서 커뮤니티 탐색, 단백질 군집화.
대표 모델: DiffPool (Ying et al., 2018b), Spectral Clustering (Tsitsulin et al., 2020).
8.1.2 물리 시스템 모델링 (Physics Modeling)
실제 물리 시스템을 시뮬레이션하는 데 사용.
예: 천체 역학 시뮬레이션, 유체 역학 예측.
대표 모델: Interaction Networks (Battaglia et al., 2016), GNN 기반 물리 모델 (Kipf et al., 2018).
8.1.3 화학 및 생물학 (Chemistry & Biology)
화합물의 특성을 분석하거나 단백질 구조를 예측하는 데 사용.
① 화합물 속성 예측 (Molecular Property Prediction)
예: 신약 개발, 화학 반응 예측.
대표 모델: GCN for Molecular Fingerprints (Duvenaud et al., 2015), Chemical Reaction Prediction (Do et al., 2019).
② 단백질 상호작용 예측 (Protein Interaction Prediction)
예: 단백질-단백질 결합 예측, 질병 원인 분석.
대표 모델: GraphCNN for Protein Interfaces (Fout et al., 2017), Side Effect Prediction (Zitnik et al., 2018).
8.1.4 지식 그래프 (Knowledge Graph)
엔티티(Entity)와 관계(Relation)를 그래프로 모델링하여 정보 검색 및 추론을 수행.
① 지식 그래프 완성 (Knowledge Graph Completion)
예: 구글 지식 그래프, 위키데이터 기반 검색.
대표 모델: R-GCN (Schlichtkrull et al., 2018), KG-BERT (Shang et al., 2019).
② 지식 그래프 정렬 (Knowledge Graph Alignment)
예: 다른 언어 간 엔티티 정렬, 데이터베이스 병합.
대표 모델: TransE 기반 GNN (Wang et al., 2018b), GCN for KG Alignment (Zhang et al., 2019d).
8.1.5 그래프 생성 (Graph Generation)
새로운 그래프를 생성하는 작업.
예: 신약 후보 물질 생성, 네트워크 확장.
대표 모델: MolGAN (De Cao & Kipf, 2018), GraphRNN (You et al., 2018).
8.1.6 조합 최적화 (Combinatorial Optimization)
최적화 문제를 해결하기 위해 그래프 기반 학습 적용.
예: 배달 경로 최적화, 스케줄링 문제 해결.
대표 모델: GNN for Travelling Salesman Problem (Nowak et al., 2018).
8.2 비구조적 시나리오 (Non-Structural Scenarios)
관계 구조가 명확하지 않은 데이터에서도 GNN을 활용할 수 있습니다.
8.2.1 이미지 처리 (Computer Vision)
이미지를 그래프로 변환하여 객체 탐지, 장면 이해, 초해상도 등의 작업 수행.
① 객체 탐지 (Object Detection)
예: 자율 주행 자동차의 사물 인식, 얼굴 인식.
대표 모델: Relation Networks for Object Detection (Hu et al., 2018).
② 장면 이해 (Scene Graph Generation)
예: 이미지 내 객체 간 관계 분석.
대표 모델: Graph R-CNN (Yang et al., 2018).
8.2.2 자연어 처리 (Natural Language Processing, NLP)
텍스트 데이터를 그래프로 변환하여 문장 간 관계를 학습.
① 문장 관계 예측 (Textual Relationship Prediction)
예: 질문 응답 시스템(QA), 기계 독해(Machine Reading Comprehension).
대표 모델: Graph-based Reading Comprehension (Tu et al., 2019).
② 기계 번역 (Machine Translation)
예: 구글 번역, AI 기반 다국어 번역 서비스.
대표 모델: Graph Convolutional Machine Translation (Gehring et al., 2017).
9. GNN의 미해결 문제 (Open Problems of GNNs)
GNN은 다양한 분야에서 큰 성과를 거두었지만, 여전히 해결해야 할 중요한 문제들이 존재합니다.
이 장에서는 GNN 연구에서 남아 있는 4가지 핵심 미해결 문제를 소개합니다.
1) 견고성 (Robustness)
GNN은 적대적 공격(Adversarial Attack)에 취약하다는 문제가 있습니다.
CNN이나 RNN과 마찬가지로 GNN도 신경망 기반 모델이므로 노이즈나 데이터 변형에 영향을 받음.
특히, 그래프 구조 자체가 변경되거나 조작될 경우(GCN, GAT 등) 성능이 급격히 저하될 수 있음.
기존 연구에서는 이미지나 텍스트에서의 적대적 공격을 GNN에 적용하는 방법을 연구했음.
관련 연구 :
GNN 공격 연구
Zügner et al. (2018): 그래프 데이터를 조작하여 GCN 성능을 저하시킬 수 있음을 보임.
Dai et al. (2018b): GNN을 직접 공격하는 새로운 방법 제안.
GNN 방어 연구
Zhu et al. (2019): GNN을 더욱 견고하게 만들기 위한 방어 전략 연구.
Sun et al. (2018): 그래프 데이터의 적대적 공격과 방어에 대한 종합적인 리뷰 제공.
2) 해석 가능성 (Interpretability)
GNN 모델은 블랙박스(Black Box) 모델이며, 출력 결과를 해석하기 어려운 문제가 있습니다.
GNN이 어떤 논리를 기반으로 특정 결과를 도출하는지 설명하는 것이 중요하지만, 현재로서는 어려움이 있음.
예를 들어, GCN이 특정 노드를 특정 클래스로 분류하는 이유를 명확하게 설명할 방법이 부족.
CNN이나 NLP 분야에서는 시각화 및 설명 가능한 AI(Explainable AI, XAI) 연구가 활발하지만, GNN에서는 아직 연구가 부족함.
관련 연구 : GNN의 해석 가능성을 높이는 연구
Ying et al. (2019): GNN 모델이 특정 예제에서 어떻게 예측을 수행했는지 설명하는 방법 제안.
Baldassarre & Azizpour (2019): GNN의 해석 가능성을 높이기 위한 프레임워크 연구.
3) 그래프 사전 학습 (Graph Pretraining)
GNN은 많은 라벨 데이터(Labelled Data)가 필요하지만, 레이블 데이터를 수집하는 것은 매우 비용이 큼.
CNN이나 NLP에서는 자기 지도 학습(Self-Supervised Learning)과 사전 학습(Pretraining)을 활용하여 데이터 부족 문제를 해결.
하지만 GNN에서는 아직 그래프 데이터를 활용한 사전 학습 기법이 정립되지 않음.
그래프 사전 학습 연구
Qiu et al. (2020), Hu et al. (2020b, 2020e): 그래프에서 사전 학습을 활용하는 방법 연구.
Zhang et al. (2020): GNN 사전 학습의 한계 및 가능성 분석.
4) 복잡한 그래프 구조 학습 (Complex Graph Structures)
현실 세계의 그래프는 다양한 구조(이질 그래프, 동적 그래프, 다중 관계 그래프 등)를 가짐.
하지만 기존 GNN 모델들은 대부분 단순한 구조(정적 그래프, 동질 그래프)에 맞춰져 있음.
해결해야 할 문제
비동형 그래프 (Heterogeneous Graphs): 다양한 유형의 노드 및 엣지를 학습하는 새로운 GNN 모델 필요.
HAN (Heterogeneous Graph Attention Network, 2019) 등의 연구가 진행됨.
동적 그래프 (Dynamic Graphs): 시간이 지남에 따라 변화하는 그래프를 학습하는 방법.
EvolveGCN (2020), TGAT (2020) 등이 제안되었으나, 여전히 개선이 필요.
다중 관계 그래프 (Multi-Relational Graphs): 지식 그래프(Knowledge Graph), 소셜 네트워크 그래프.
R-GCN (Relational GCN, 2018)**이 대표적인 연구지만, 아직 해결해야 할 과제가 많음.
그래프의 개요 및 분류에 대한 논문 요약이었습니다.
마지막으로 PyG의 주요 모듈과 논문 정보입니다.
PyG 모듈과 관련 논문 연혁
PyG 모듈모델명 (논문 명칭)연도논문 링크
| GCNConv | GCN (Graph Convolutional Network) | 2017 | Kipf & Welling (2017) |
| GATConv | GAT (Graph Attention Network) | 2018 | Veličković et al. (2018) |
| SAGEConv | GraphSAGE (Sample and Aggregates) | 2017 | Hamilton et al. (2017) |
| GINConv | GIN (Graph Isomorphism Network) | 2019 | Xu et al. (2019) |
| SGConv | SGC (Simplifying Graph Convolution) | 2019 | Wu et al. (2019) |
| APPNP | APPNP (Approximate Personalized Propagation of Neural Predictions) | 2019 | Klicpera et al. (2019) |
| TAGConv | TAGCN (Topology Adaptive Graph Convolutional Network) | 2018 | Du et al. (2018) |
| ChebConv | ChebNet (Chebyshev Spectral GCN) | 2016 | Defferrard et al. (2016) |
| GatedGraphConv | GGNN (Gated Graph Neural Networks) | 2015 | Li et al. (2015) |
| GraphConv | GraphConv (General Graph Convolution) | 2018 | Morris et al. (2018) |
| TransformerConv | Graph Transformer | 2021 | Dwivedi & Bresson (2021) |
| EdgeConv | Dynamic Graph CNN (DGCNN) | 2019 | Wang et al. (2019) |
| GCN2Conv | GCNII (Graph Convolutional Networks II) | 2020 | Chen et al. (2020) |
| ARMAConv | ARMA (Auto-Regressive Moving Average Graph Neural Network) | 2019 | Bianchi et al. (2019) |
| ClusterGCNConv | ClusterGCN (Scalable GCN for Large Graphs) | 2019 | Chiang et al. (2019) |
| GraphUNet | Graph U-Net | 2019 | Gao & Ji (2019) |
| DeepGCNLayer | DeepGCNs (Residual and Dense Graph Networks) | 2019 | Li et al. (2019) |