두개의 독립된 모집단의 평균을 구할때 사용한다.
가정
정규성(두 모집단은 정규성을 만족한다.)
등분산성(두 집단의 분산은 같다)
가설
귀무가설 H0 : 두 집단의 모평균은 같다.
대립가설 H1 : 두 집단의 모평균은 차이가 있다.

독립표본은 표본의 개수와 모분산 여부에따라 3가지 로 구분된다.
1. 표본의 개수가 충분하고, 모분산을 알 경우 (Z)
2. 표본의 개수가 충분하고, 모분산을 모르는 경우(T)
3. 표본의 개수가 충분하지 않고, 모분산을 모르는 경우
1. 표본의 개수는 충분하고, 모분산을 아는 경우
검정통계량 : 귀무가설이 두집단의 모평균은 같다이기 때문에 모평균의 차는 0이어서 다음과 같이 표시된다.
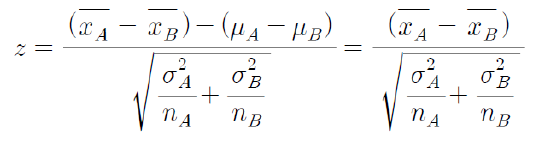
신뢰구간
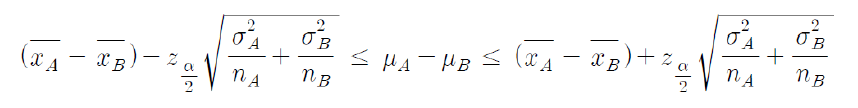
* 현실세계에서는 모분산을 알수 있는 경우가 없다.
2. 표본의 개수는 충분하고, 모분산을 모르는 경우
검정통계량

신뢰구간

3. 등분산 검정
t검정에서 독립표본, 즉 2개 집단의 평균을 비교할 때, 등분산에 따라 위와 같이 계산식이 바뀐다.
분산이 같을 경우, 합동분산을 이용하여 검정통계량을 계산한다.
분산이 같은경우는 검정통계량은 Z검정과 계산 방식은 동일하나 자유도는 2개 집단의 표본개수중 작은 표본 개수의 -1을 사용하게 된다.
그래서 등분산 여부가 중요한데, 등분산 검정에서는 크게 아래 2개를 사용한다.
(1) levene : 데이터의 중앙값 주변의 변동성을 비교하여 등분산을 검정한다.
(2) bartlett : 데이터의 분산을 비교하여 등분산을 비교한다.
즉, 데이터가 정규분포를 따르면 주로 bartlett를 사용하고, 그렇지 않은경우는 levene를 사용한다.
# 집단 1 : 평균이 3, 표준편차 2이고 10개인 표본
# 집단 2 : 평균이 5, 표준편차 3이고 20개인 표폰
x1 = np.random.normal(loc=3, scale=2, size=10)
x2 = np.random.normal(loc=5, scale=3, size=20)
H0 = 합동분산. H1 = 이분산.
# 바틀렛 테스트.
from scipy.stats import bartlett
bartlett(x1,x2)
BartlettResult(statistic=0.3389054312181491, pvalue=0.560461710131561)
# levene테스트
from scipy.stats import levene
levene(x1, x2)
LeveneResult(statistic=0.43890976312008173, pvalue=0.5130659504885586)
# 둘다 pvalue가 0.05보다 크므로 귀무가설을 기각, 등분산을 사용하여 합동분산을 사용한다.
예제문제
iris의 setosa와 versicolor 의 sepal length의 평균은 차이가 있다를 가설 검정하고자 한다.
1. setasa와 versicolor 는 정규성을 만족하는가?
2. setasa와 versicolor 는 등분산을 만족하는가?
3. 두 집단의 평균은 같은지 검정하라.
4. 이 때 검정통계량
5. 신뢰구간을 구하라.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
df = sns.load_dataset('iris')
setosa = df.loc[df.species =='setosa','sepal_length' ]
versicolor = df.loc[df.species =='versicolor','sepal_length']
# 1. 정규성 확인
from scipy.stats import shapiro
shapiro(setosa), shapiro(versicolor)
(ShapiroResult(statistic=0.9776982069015503, pvalue=0.4595010578632355),
ShapiroResult(statistic=0.9778357148170471, pvalue=0.4647378921508789))
# 귀무가설 : 두 독립변수는 정규성을 만족한다.
# 대립가설 : 두 독립변수는 정규성을 만족하지 않는다.
# 두 변수 모두 pvalue가 모두 유의수준 0.05보다 커서 정규성을 만족한다.
# 2. 등분산 확인
from scipy.stats import levene
levene(setosa,versicolor)
LeveneResult(statistic=8.172720533728683, pvalue=0.005195521631017526)
# pvalue가 0.05보다 작아, 등분산을 만족하지 않는다.
# 3. 두평균이 같은지 검증하라
from scipy.stats import ttest_ind
ttest_ind(setosa, versicolor, equal_var=True) # 등분산일 경우
Ttest_indResult(statistic=-10.52098626754911, pvalue=8.985235037487079e-18)
ttest_ind(setosa, versicolor, equal_var=False) # 등분산이 아닌경우
Ttest_indResult(statistic=-10.52098626754911, pvalue=3.746742613983842e-17)
# 등분산이 아니므로 equal_val=False이고, pvalue가 0.05보다 작아 귀무가설을 기각한다.
# setosa와 versicolor의 sepal length의 평균은 유의한 차이가 있다.
# 4. 검정통계량을 구하라.
# ttest_ind의 statistic=-10.52098626754911값이 검정 통계량이다.
# 수식으로 풀어보면
# setosa 평균
mean1 = setosa.mean()
# versicolor 평균
mean2 = versicolor.mean()
# versicolor와 setosa의 표준오차
sem = ((setosa.sem()**2) + (versicolor.sem()**2))**0.5
mean1, mean2, sem
(5.006, 5.936, 0.08839475466938762)
# 두개의 평균차를 공통 표준오차로 나눈다.
(mean1 - mean2)/sem
-10.52098626754911
# ttest_ind의 검정통계량과 같음을 알 수 있다.
# 5. 95% 신뢰구간을 구하라.
# versicolor와 setosa의 표준오차
sem = ((setosa.sem()**2) + (versicolor.sem()**2))**0.5
mean_diff = (mean1 - mean2)
print('mean diff:',mean_diff, "sem :" ,sem )
mean_diff - 1.96/sem, (mean1 - mean2) + 1.96/sem
mean diff: -0.9299999999999997 sem : 0.08839475466938762
(-23.10326138107125, 21.24326138107125)
3. 표본의 개수가 부족하고 모분산을 모르는 경우
검정통계량
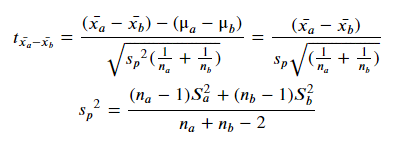
신뢰구간
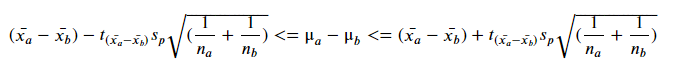
연습문제
A공장과 B공장의 불량품 개수의 평균차이를 검증한다.
A공장 [3,4,6,5,5]
B공장 [7,6,8,7,5,8]
1. 검정통계량을 구하라.
2. 신뢰구간을 구하라.
3. 평균이 같은지 검증하라.
import numpy as np
x1 = [3,4,6,5,5]
x2 = [7,6,8,7,5,8]
# 1. 검정통계량
df = (len(x1)+len(x2)-2) # 자유도는 n-2
common_var = ((len(x1)-1)*np.var(x1, ddof=1) + (len(x2)-1)*np.var(x2, ddof=1)) / df
t_stat = (np.mean(x1) - np.mean(x2)) / (common_var * (1/len(x1)+1/len(x2)))**(1/2)
t_stat
-3.1896726452700257 # 검정통계량
# 2. 신뢰구간
from scipy.stats import t
tval = t.ppf(0.05/2,df=df)
mean_diff = (np.mean(x1) - np.mean(x2))
common_var = ((len(x1)-1)*np.var(x1, ddof=1) + (len(x2)-1)*np.var(x2, ddof=1)) / df
mean_diff - tval*(common_var * (1/len(x1)+1/len(x2)))**(1/2), mean_diff + tval*(common_var * (1/len(x1)+1/len(x2)))**(1/2)
(-0.6494244001454514, -3.817242266521215)
# 3. 평균이 같은지 검증하라.
tval = t.ppf(0.05/2,df=df)
-2.262157162740992 # 기각역
t_stat
-3.1896726452700257 # 검정통계량
# 검증통계량이 크므로 평균이 같다는 귀무가설을 기각한다.
예제2
import numpy as np
# 집단 1 : 평균이 3, 표준편차 2이고 10개인 표본
# 집단 2 : 평균이 5, 표준편차 3이고 20개인 표폰
np.random.seed(1234)
x1 = np.random.normal(loc=3, scale=2, size=10)
x2 = np.random.normal(loc=5, scale=3, size=20)
# 바틀렛 테스트. H0 = 합동분산. H1 = 이분산.
from scipy.stats import bartlett
print('등분산:',bartlett(x1,x2))
from scipy.stats import ttest_ind
print(ttest_ind(x1, x2, equal_var=True))
# 두 표본의 평균
mean_x1 = np.mean(x1)
mean_x2 = np.mean(x2)
# 두 표본의 크기
n1 = len(x1)
n2 = len(x2)
# 합동분산 계산
combined_variance = ((len(x1) - 1) * x1.var(ddof=1) + (len(x2) - 1) * x2.var(ddof=1)) / (len(x1) + len(x2) - 2)
# t-검정 통계량 계산
t_statistic = (mean_x1 - mean_x2) / np.sqrt(combined_variance * (1/n1 + 1/n2))
from scipy.stats import t
pval = t.cdf(t_statistic, df=n1+n2-2)*2
print('t_statistic:',t_statistic,'pvalue:',pval)
등분산: BartlettResult(statistic=1.041352162617009, pvalue=0.3075072030767705)
Ttest_indResult(statistic=-2.34826097302615, pvalue=0.026154169650038642)
t_statistic: -2.34826097302615 pvalue: 0.026154169650038642
# 신뢰구간 계산
# t 분포의 임계값(예: 95% 신뢰수준에서)을 찾기
confidence_level = 0.95
alpha = 1 - confidence_level
df = (n1 + n2 - 2)
t_critical = t.ppf(1 - alpha/2, df=df)
meandiff = mean_x1 - mean_x2
# 표준 오차 계산
standard_error = np.sqrt(combined_variance * (1/n1 + 1/n2))
# 신뢰구간
confidence_interval = (meandiff - t_critical * standard_error, meandiff + t_critical * standard_error)
print(confidence_interval)
print(t.interval(confidence=confidence_level, loc=mean_x1 - mean_x2 , scale=standard_error, df=(n1 + n2 - 2) ))
(-4.755142622072546, -0.32430187952354705)
(-4.755142622072546, -0.32430187952354705)'통계' 카테고리의 다른 글
| 통계적 추론 (1) | 2023.10.30 |
|---|---|
| QQ Plot (0) | 2023.10.29 |
| 모수 유의성 검정(Significance test) (1) | 2023.10.11 |
| 가우시안 혼합 분포 군집(GaussianMixture) (0) | 2023.09.26 |
| 일원분석분산(One-way ANOVA) (0) | 2023.09.20 |