정규분포는 평균을 중심으로 대칭이며, 종모양(bell shape)의 확률 밀도를 갖는 분포이다.
정규분포의 모양과 위치는평균과 표준편차에 의해 결정된다.
확률 밀도 함수는 면적이 확률이되고, 전체 면적은 1이다.
파라미터 : µ (평균), σ²(분산)
확률변수표기 : X ~ N(µ , σ²)
기대값 : µ
분산 : σ²

Scipy의 norm 주요 함수
1. pdf : Probability density function.
pdf(x, loc=0, scale=1)
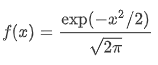
정규분포의 확률 밀도 함수이다.
2. cdf(x, loc=0, scale=1) : Cumulative distribution function.
누적 확률 분포함수이다. 특정 x값에서의 확률을 계산할 수 있다.
3. sf(x, loc=0, scale=1) : Survival function
생존함수라고 하는데 1 - cdf값이다. x 지점에서 남아있는 확률이다.
4. ppf(q, loc=0, scale=1) : Percent point function
특정 분위의 x값을 찾을 수 있다. 예를 들어 75%의 z값등을 구할때
5. rvs(loc=0, scale=1, size=1, random_state=None) : Random variates.
size개수 만큼, 정규분포인 random 값을 return한다.
6. interval(confidence, loc=0, scale=1) : Confidence interval
신뢰구간의 하한값 및 상한값을 반환한다. ex) norm.interval(0.95, loc = 10, scale = 2)
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
mu =100
sigma = 2
size = 1000
x = np.linspace(90, 110, size)
plt.figure(figsize=(8,3))
plt.subplot(2,2,1)
plt.hist(norm.rvs(loc=mu, scale=sigma, size=size), bins=150)
plt.title("Random(RVS)")
plt.subplot(2,2,2)
plt.plot(x, norm.pdf(x, loc=mu, scale=sigma))
plt.title("PDF")
plt.subplot(2,2,3)
plt.plot(x, norm.cdf(x, loc=mu, scale=sigma))
plt.title("CDF")
plt.subplot(2,2,4)
plt.plot(x, norm.sf(x, loc=mu, scale=sigma))
plt.title("SF")
plt.show()
평균이 100이고, 표준편차가 2인 정규분포 곡선을 그리면 아래와 같다.
4 표준편차 90~100 이내에 99.9% 이상의 데이터가 포함된다.
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
mu = 100 # 평균
sigma = 2 # 표준편차
histdata = np.random.normal(loc=mu, scale=sigma, size=1000000)
# numpy random함수로 100만개의 random 정규 분포 데이터를 생성한다.
x = np.linspace(90,110,1000) # 그래프의 x 데이터를 생성한다. 90과 110사이 1000개 데이터
y = stats.norm.pdf(x, loc=mu, scale=sigma) # scipy 의 정규분포 확률 밀도 함수로 y값을 계산한다.
# numpy 의 random함수로 nomal distribution random value생성 히스토그램
plt.hist(histdata, bins=1000, density=True, alpha=0.6)
# scipy 의 normal distribution random value 생성
plt.plot(x,y)
# 평균
plt.axvline(histdata.mean(), color="red", linestyle='--')
plt.text(histdata.mean()+0.1,0.21, "Mean", color="red")
# 표준편차
plt.axvline(histdata.mean()-histdata.std(), color="green", linestyle='--')
plt.axvline(histdata.mean()+histdata.std(), color="green", linestyle='--')
plt.axvline(histdata.mean()-2*histdata.std(), color="green", linestyle='--')
plt.axvline(histdata.mean()+2*histdata.std(), color="green", linestyle='--')
plt.axvline(histdata.mean()-3*histdata.std(), color="green", linestyle='--')
plt.axvline(histdata.mean()+3*histdata.std(), color="green", linestyle='--')
plt.text(histdata.mean()+histdata.std()+0.1,0.21, "Std", color="green")
plt.show()
표준정규분포 (Standard Normal Distribution)
정규분포 중 µ = 0, σ² = 1인 정규분포 (평균이 0 분산이 1인 정규분포)
파라미터 : 0, 1
확률변수표기 : Z ~ N(0 , 1)
기대값 : 0
분산 : 1
예제문제 1:
평균이 15 , 표준편차가 5일 인 정규분포에서 (1) X가 25보다 작을 확률과 X가 10보다 크고 25보다 작을 확률
풀이
from scipy.stats import norm
# cdf x, loc, scale
norm.cdf(25, loc=15, scale=5)
--> 0.9772
norm.cdf(25, loc=15, scale=5) - norm.cdf(10, loc=15, scale=5)
--> 0.8186
예제문제2
평균 65, 표준편차 10인 정규분포에서
(1) X가 50이하의 비율
from scipy.stats import norm
norm.cdf(50, loc=65, scale=10)*100
# 6.68
(2) 상위 20%의 X값
norm.ppf(0.8, loc=65, scale=10)
# 73.416
예제문제3
고등학교 남학생 키의 평균이 172, 표준편차가 8인 정규 분포 일 때 95% 신뢰구간값은?
norm.interval(0.95, loc=172, scale=8)
(156.32028812367957, 187.67971187632043)
예제문제4
수학시험의 평균이 63이고, 표준편차가 10인 정규분포일 때 점수가 50점 이하일 확률과 성적이 상위 10%일 점수는?
(1)norm.cdf(50, loc=63, scale=10)
0.09680048458561036
(2) norm.ppf(0.9, loc=63, scale=10)
75.815515655446
'통계' 카테고리의 다른 글
| 이상치 처리 (0) | 2023.06.17 |
|---|---|
| 신뢰구간(Confidnce Interval) 파이썬 (0) | 2023.06.10 |
| 표준정규분포 (Standard Normal Distribution) (0) | 2023.06.06 |
| 포아송분포(Poisson Distribution) (1) | 2023.06.06 |
| 이항분포 (Binormal Distribution) (0) | 2023.06.06 |