Title: "Variational Graph Auto-Encoders"
Authors: Thomas N. Kipf, Max Welling
Published: 2016
논문 링크: https://arxiv.org/abs/1611.07308
GAE 구현 코드: https://github.com/tkipf/gae
"Variational Graph Auto-Encoders" 논문은 Graph Autoencoder(GAE)와 Variational Graph Autoencoder(VGAE)를 소개하며, 그래프 데이터의 노드 임베딩을 학습하는 방법을 제안하였습니다.
그래프의 구조를 유지하면서 각 노드의 저차원 임베딩을 학습하여, 링크 예측(link prediction)이나 그래프 복원(graph reconstruction)을 수행합니다.
논문 내용이 3페이지로 아래는 논문 내용을 번역해 보았습니다.
Variational Graph Auto-Encoders 번역
1) A latent variable model for graph-structured data(그래프 구조화 데이터를 위한 잠재 변수 모델)
변분 그래프 오토인코더(VGAE)를 소개합니다.
이는 변분 오토인코더(VAE)[2,3]에 기반한 프레임워크로, 그래프 구조 데이터를 비지도 학습하는 모델입니다.
이 모델은 잠재 변수를 활용하며, 방향이 없는 그래프에 대한 해석 가능한 잠재 표현을 학습할 수 있습니다(그림 1 참고).
이 모델을 그래프 컨볼루션 네트워크(GCN) 인코더와 간단한 내적 디코더를 사용하여 구현합니다.
이 모델은 논문 인용 네트워크의 링크 예측을 수행하여, VGAE가 경쟁력 있는 성능을 보였습니다.
기존의 그래프 구조 데이터와 링크 예측[5,6,7,8]을 위한 대부분의 비지도 학습 모델과 달리, 우리 모델은 노드 특징을 자연스럽게 통합해서, 여러 벤치마크 데이터셋에서 예측 성능을 크게 향상 시킬수 있었습니다.
* 잠재변수(Latent Variable) : 직접 관측할 수 없지만, 데이터의 패턴이나 구조를 설명하는 데 중요한 역할을 하는 숨겨진 변수

정의(Definitions)
방향이 없고, 가중치가 없는 그래프 G=(V,E) 가 주어집니다. 여기서 N=∣V∣ 는 노드의 개수를 의미합니다.
그래프G 의 인접 행렬 A 를 정의하고, 대각 원소를 1로 설정합니다.(즉, 각 노드는 자기 자신과 연결).
또한, A 의 차수 행렬 D를 정의합니다.
추가적으로, 확률적 잠재 변수 $z_i$를 정의하여, 이는 N×F 크기의 행렬 Z로 요약하고 노드 특징은 N×D 크기의 행렬 X로 정의합니다.
(* F는 잠재변수의 개수로, 저차원 임베딩의 차원 수입니다. 사용자가 임의로 설정할수 있는 하이퍼 파라미터로 논문에서는 F=16으로 사용했습니다, 즉 N×D크기의 X를 N×F크기의 잠재 변수 행렬 Z를 생성합니다 )
추론 모델 (Inference Model)
두 개의 층으로 구성된 GCN으로 매개변수화된 간단한 추론 모델을 사용합니다:
$q(Z | X, A) = \prod_{i=1}^{N} q(z_i | X, A), \quad \text{where} \quad q(z_i | X, A) = \mathcal{N}(z_i | \mu_i, \text{diag}(\sigma_i^2))$
여기서 $\mu=\text{GCN}_{\mu}(X,A)$ 는 평균 벡터들의 행렬 $\mu_i$ 이며,
유사하게 $\log \sigma = GCN_\sigma(X, A)$ 입니다.
이 두 개 층으로 이루어진 GCN은 다음과 같이 정의됩니다:
$\text{GCN}(X, A) = \tilde{A} \text{ReLU}(\tilde{A} X W_0) W_1$
여기서, $W_0$ 및 $W_1$ 은 가중치 행렬입다.
또한,$\text{GCN}_\mu(X, A)$ 와 $\text{GCN}_\sigma(X, A)$는 첫 번째 층의 매개변수 $W_0$ 를 공유합니다.
$tilde{A} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$는 대칭 정규화된 인접 행렬입니다.
*
parameterized inference model 이라는 용어가 헷갈리는데, 정리하면 잠재변수 Z를 학습하기 위해 GCN을 기반으로 Z의 분포를 예측하는 모델, 즉 Z를 학습하기 위해 W0와 W1을 최적화 하는 모델정도로 이해됩니다.
논문에서 inference model은 잠재변수 Z의 분포를 추정하는 역할입니다.
q(Z|X,A)는 잠재변수 Z의 의 확률 분포로 평균 $\mu$ ,
분산 ${\sigma}^2$를 따르는 정규 분포를 따릅니다.
평균과 로그분산은 아래 수식에 대해 정의됩니다.
평균
$\mu= \text{GCN}_{\mu}(X, A)=\tilde{A}\text{ReLU}(\tilde{A}XW_0)W_1^\mu$
로그 분산
$\log \sigma = GCN_\sigma(X, A)=\tilde{A}\text{ReLU}(\tilde{A}XW_0)W_1^\sigma$
즉, GCN의 W0, W1을 이용해 Z이 확률분포를 계산하는 모델로 해석됩니다.
생성 모델(Generative Model)
생성 모델은 잠재 변수 간의 내적(inner product)에 의해 정의됩니다:
$p(A | Z) = \prod_{i=1}^{N} \prod_{j=1}^{N} p(A_{ij} | z_i, z_j)$
여기서,
$p(A_{ij} = 1 | z_i, z_j) = \sigma(z_i^T z_j)$
이며, $A_{ij}$ 는 인접 행렬 A 의 원소이고, σ(⋅) 는 시그모이드 함수입니다.
* 잠재변수 z를 이용하여 그래프의 구조 즉 인접 행렬 A를 생성(복원)하는 의미입니다.
즉, 잠재변수 zi와 zj를 이용해, p(Aij)는 인접행렬 A의 i행과 j열의 edge가 있을지의 확률을 의미합니다.
Z를 N*F 로 정의해서, $ZZ^T$ 를 수행하면, N*N의 인접행렬 A의 예측값이 만들어집니다.
학습(Learning)
우리는 변분 하한(variational lower bound)$ \mathcal{L}$을 최적화하여 학습을 진행합니다.
이를 변분 파라미터 $W_i$ 에 대해 다음과 같이 정의합니다:
$\mathcal{L} = \mathbb{E}_{q(Z | X, A)} \left[ \log p(A | Z) \right] - KL \left[ q(Z | X, A) || p(Z) \right]$
여기서,
- $KL[q(\cdot) || p(\cdot)]$ 는 q(⋅) 과 p(⋅)사이의 Kullback-Leibler( KL) 발산입니다.
- 우리는 정규분포(Gaussian prior) 를 사용하여 p(Z) 를 다음과 같이 설정합니다:
$p(Z) = \prod_{i} p(z_i) = \prod_{i} \mathcal{N}(z_i | 0, I)$
- 매우 희소한(sparse) 인접 행렬 A 의 경우, $\mathcal{L}$의 항들 중 $A_{ij} = 1$ 인 요소의 가중치를 조정하거나, $A_{ij} = 0$ 인 요소를 부분 샘플링하는 방식이 유용할 수 있습니다.
- 우리는 후자 대신 $A_{ij}=1$ 인 항들의 가중치를 조정하는 방법을 선택하여 실험을 진행합니다.
- 우리는 full-batch gradient descent 을 수행하며, 학습을 위해 재매개변수화 트릭(reparameterization trick) [2]을 사용합니다.
- 특징 없는(featureless) 접근 방식을 적용하려면, X 에 대한 의존성을 제거하고 GCN에서 X 를 단위 행렬(Identity matrix)로 대체하면 됩니다.
비확률적 그래프 오토인코더(GAE) 모델
변분 그래프 오토인코더(VGAE)의 비확률적(non-probabilistic) 변형인 그래프 오토인코더(GAE) 모델에서는 잠재 표현 Z 를 계산한 후, 복원된 인접 행렬 $\hat{A}$ 를 다음과 같이 정의합니다:
$\hat{A} = \sigma(ZZ^T)$
여기서, 잠재 표현 Z 는 다음과 같이 그래프 컨볼루션 네트워크(GCN)를 사용하여 계산됩니다:
$Z = \text{GCN}(X, A)$
* COMMENT
논문이 짧은 만큼 내용이 많이 압축되어있습니다.
변분 하한(variational lower bound): 간단하게 설명하면 VAE등의 사용되는 핵심 개념으로 복잡한 확률분포 p(x)를 집접 사용하기 어려울 때, 보다 단순한 분포 q(x)를 사용하여 근사하는 방법입니다.
Loss function의 개념으로 생각하면 편리합니다.
$\mathcal{q} = \mathbb{E}_{q(Z)} \left[ \log p(X | Z) \right] - KL \left[ q(Z) || p(Z) \right]$
이 값을 최대화하면 로그 가능도 logp(X)를 최대화하는 효과를 얻을 수 있습니다.
첫번째 항 : 재구성 오차
A를 재구성한 예측값과, 실제 A값의 차이를 cross binary entropy하는 공식입니다.
A와 예측한 pred_A를 비교하여 Binary Cross-Entropy(BCE) Loss를 사용합니다.
이항을 사용하면 VGAE가 원래의 그래프를 잘 복원하도록 학습되었다는 의미입니다.
q(Z|X, A) : GCN 인코더가 학습한 Z의 분포를 의미합니다.p(A|Z) : Z를 복원하여 A의 복원한 예측확률입니다.E(Z|X,A): 여러개의 Z를 샘플링(reparameterization trick)하여 평균적인 성능을 평가합니다.
두번째항 : KL Divergence(Kullback-Leibler발산)
두개의 확률 분포가 얼마나 다른지를 측정하는 지표입니다
$KL(q(x)||p(x)) = \sum_x q(x) log \frac{q(x)}{p(x)}$
VGAE에서는 잠재변수 Z의 분포 q(Z|X,A)가 정규분포 P(Z) = N(0,1)과 비슷해지도록 만들기 위해 KL Divergence를 사용합니다.
첫번째 항은 인접행렬 A를 잘 복원하도록 학습하고, 두번째 항은 Z가 정규분포를 따르도록 학습한다고 이해하면 됩니다.
2. 링크 예측 실험(Experiments on link prediction)
우리는 VGAE 및 GAE 모델이 의미 있는 잠재 임베딩을 학습할 수 있는지를 검증하기 위해 여러 유명한 논문 인용 네트워크(citation network) 데이터셋에서 링크 예측(link prediction) 작업을 수행하였습니다.
본 실험에서는 일부 논문 간 인용 관계(엣지)를 제거한 상태에서 모델을 학습하며, 모든 노드의 특징(feature)은 유지됩니다. 이후, 제거된 엣지와 동일한 수의 무작위로 선택된 비연결 노드 쌍(non-edges) 을 활용하여 검증(validation) 및 테스트(test) 세트를 구성하였습니다.
모델의 성능 평가는 실제 엣지(연결)와 비엣지(비연결)를 올바르게 분류하는 능력을 기준으로 진행하였습니다.
- 검증 세트(validation set): 인용 링크의 5%
- 테스트 세트(test set): 인용 링크의 10%
- 검증 세트는 하이퍼파라미터 최적화(hyperparameter tuning) 에 사용됩니다.
비교 모델
우리는 다음과 같은 두 개의 대표적인 벤치마크 모델과 VGAE/GAE 모델을 비교하였습니다.
- Spectral Clustering (SC) [5]:
- 노드 임베딩 Z 을 제공하는 방법으로, 고유 벡터(eigenvector) 기반 기법을 사용합니다.
- DeepWalk (DW) [6]:
- 그래프 내 노드 임베딩을 학습하는 비지도 학습 방식으로, 랜덤 워크(random walk)를 기반으로 합니다.
SC와 DW는 노드 임베딩 Z 를 생성하는 방법이며, 우리는 아래와 같은 방식으로 링크 예측 점수를 계산하였습니다:
$\hat{A}_{ij} = \sigma(Z Z^T)$
(여기서, σ(⋅) 는 시그모이드 함수)
참고로, DW의 최근 변형 모델들 [7, 8]은 성능이 유사하므로 본 실험에서 제외하였습니다.
또한, SC 및 DW는 입력 특징(input features) 을 활용하지 않는 모델입니다.
실험 설정 및 하이퍼파라미터
- VGAE 및 GAE:
- 가중치는 [9]의 방법을 따라 초기화하였습니다.
- 200번의 반복(iteration) 동안 학습을 진행하였습니다.
- Adam 옵티마이저(Adam optimizer) [10] 를 사용하였으며, 학습률(learning rate)은 0.01로 설정하였습니다.
- 모든 실험에서 32차원(hidden layer) 은닉층과 16차원(latent variables) 잠재 변수를 사용하였습니다.
- Spectral Clustering (SC):
- [11]의 구현을 사용하였으며, 임베딩 차원은 128로 설정하였습니다.
- DeepWalk (DW):
- [8]의 공식 구현을 사용하였으며, 기존 논문에서 설정한 기본값을 적용하였습니다.
- 임베딩 차원: 128
- 랜덤 워크(random walks): 노드당 10개의 경로, 각 경로의 길이는 80
- 컨텍스트 크기(context window size): 10
- 학습 에포크(epochs): 1
Discussion
논문 인용 네트워크에서 링크 예측 작업에 대한 실험 결과는 표 1에요약하였습니다.
GAE*와 VGAE*는 입력 특징(input feature)을 사용하지 않은 실험을, GAE와 VGAE는 입력 특징을 사용한 실험을 나타냅니다.
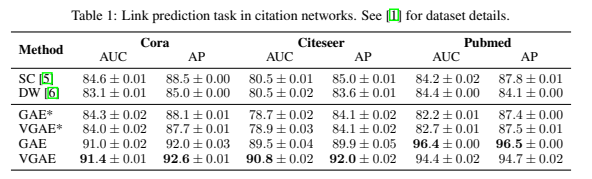
테스트 세트의 각 모델에 대한 ROC 곡선 아래 면적(AUC)과 평균 정밀도(AP, Average Precision) 점수를 츨정하였습니다.
결과는 고정된 데이터 세트 분할에 대해 무작위로 초기화하여 10회 실행한 평균 결과와 표준 오차를 나타냅니다.
VGAE와 GAE 모두 입력 특징이 없는 조건에서 기존 모델과 경쟁력 있는 결과를 달성합니다.
하지만, 입력 특징(input features)를 추가하면 데이터 세트 전반에서 예측 성능이 크게 향상되었습니다.
VGAE는 가우시안 사전분포(Gaussian prior)는 내적 디코더와 함께 사용하면, 임베딩 벡터를 영중심(원점)에서 멀리 떨어진곳으로 분포시키는 경향을 가지기 때문에 좋지 않은 선택이 될 수 있습니다(그림 1 . 참조)
그럼에도 불구하고 VGAE 모델은 Cora와 Citeseer 데이터 세트 모두에서 더 높은 예측 성능을 보였습니다.
향후 연구에서는 더 적합한 사전 분포, 더 유연한 생성 모델, 확장성 향상을 위한 확률적 경사 하강 알고리즘의 적용을 조사할 예정입니다.
GAE와 VGAE의 차이점
논문에서는 설명이 일부 나와있는데 다음과 같은 차이점이 있습니다.
강화학습에서 deterministic과 stochastic을 언급했는데, 잠재변수 Z를 결정론적으로 정의할지 확률론적으로 사용할지의 차이입니다. GAE에서는 Z를 sigma(Z@Z.T)로 정의하는데 비해 VGAE에서는 Z를 가우시안 분포의 샘플링으로 정의합니다. GAE에서는 KL-divergence loss를 사용하지 않고 첫번째 항(binary cross entropy)만 사용합니다.
VGAE가 GAE보다 불확실성을 고려한 더 강건한 임베딩을 제공합니다.
| 모델 | 잠재변수 | 손실함수 | 특징 |
| GAE | Deteministic | BCE | 직접적인 임베딩 학습 |
| VGAE | Stochastic(평균, 분산) | BCE + KL-divergence | 불확실성을 고려한 확률적 임베딩 학습 |
VGAE 코딩
torch_geometric를 이용한 예제코드를 작성합니다.VGAE를 사용할 때는 사용자가 직접 Encoder모델을 정의해야합니다. VGAE에는 인코더가 포함되어있지 않고, GCN외 GraphSAGE등 다른 모델도 사용할 수 있게 합니다.
- 사용자 정의 인코더 (VariationalGCNEncoder)
- conv1: 노드 특징을 변환하는 GCN 레이어
- conv_mu: 평균(μ) 학습
- conv_logstd: 로그분산(log σ²) 학습
- 인코더의 출력은 (μ, logσ²) 두 개의 값
- 샘플링 (Reparameterization Trick)
- VGAE는 내부적으로 μ+σ⋅ϵ 샘플링을 수행
- 이 과정에서 정규분포에서 샘플링된 노이즈 ϵ∼N(0,I) 사용
- 디코더 (Decoder)
- VGAE는 내적(inner product)을 사용하여 인접 행렬을 복원
- A^=σ(Z@Z.T)를 통해 그래프 구조를 예측
- 손실 함수 (Loss)
- model.recon_loss(z, edge_index): 그래프 복원 오차 (Binary Cross Entropy)
- model.kl_loss(): 가우시안 분포와의 KL-divergence
논문에서는 없지만 torch_geometric에서 손실함수 KL에 1/N을 곱하도록 하고 있습니다.
그래프의 크기가 커질 수록 KL손실이 커져서 재구성 손실과의 균형이 깨지는 문제가 발생되어 1/N을 곲해 정규화 합니다.
논문에서는 전체 그래프를 학습하는 full-batch를 수행하는데, 미니배치 학습으로 구현됩니다.
성능은 AUC와 AP(Average Precision)을 측정합니다. AP는 Precision-Recall곡선의 아래 면적으로 Poistive를 얼마나 잘 예측하는지를 의미합니다. 둘다 1에 가까울 수록 높은 성능을 나타냅니다.
import numpy as np
import torch
import torch.nn.functional as F
import torch_geometric.transforms as T
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv, VGAE
# Cora 데이터셋을 Train 0.85, val 0.05, test 0.1 생성
transform = T.Compose([T.NormalizeFeatures(), T.RandomLinkSplit(num_val=0.05, num_test=0.1, is_undirected=True, split_labels=True, add_negative_train_samples=False)])
dataset = Planetoid('.', name='Cora', transform=transform)
train_data, val_data, test_data = dataset[0]
class Encoder(torch.nn.Module):
def __init__(self, din, dout):
super().__init__()
self.conv1 = GCNConv(din, 2*dout) # W0 학습 : 공유
self.conv_mu = GCNConv(2*dout, dout) # W1의 평균 학습
self.conv_logstd = GCNConv(2*dout, dout) # W1의 분산 학습
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = F.relu(x)
mu = self.conv_mu(x, edge_index)
logstd = self.conv_logstd(x, edge_index)
return mu, logstd
model = VGAE(Encoder(dataset.num_features, 16))
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
@torch.no_grad()
def test(data):
model.eval()
z = model.encode(data.x, data.edge_index)
return model.test(z, data.pos_edge_label_index, data.neg_edge_label_index)
for epoch in range(301):
model.train()
optimizer.zero_grad()
Z = model.encode(train_data.x, train_data.edge_index)
loss = model.recon_loss(Z, train_data.pos_edge_label_index) + (1/train_data.num_nodes)*model.kl_loss()
loss.backward()
optimizer.step()
if epoch%50 == 0:
val_auc, val_ap = test(val_data)
print(f'Epoch {epoch:>2} | Loss: {loss:.4f} | Val AUC: {val_auc:.4f} | Val AP: {val_ap:.4f}')
test_auc, test_ap = test(test_data)
print(f'Test AUC: {test_auc:.4f} | Test AP {test_ap:.4f}')
Epoch 0 | Loss: 3.4245 | Val AUC: 0.6656 | Val AP: 0.6806
Epoch 50 | Loss: 1.3132 | Val AUC: 0.6656 | Val AP: 0.6792
Epoch 100 | Loss: 1.1394 | Val AUC: 0.7073 | Val AP: 0.7088
Epoch 150 | Loss: 1.0639 | Val AUC: 0.7717 | Val AP: 0.7683
Epoch 200 | Loss: 0.9788 | Val AUC: 0.8609 | Val AP: 0.8535
Epoch 250 | Loss: 0.9469 | Val AUC: 0.8887 | Val AP: 0.8881
Epoch 300 | Loss: 0.9177 | Val AUC: 0.8970 | Val AP: 0.8996
Test AUC: 0.8959 | Test AP 0.8952
